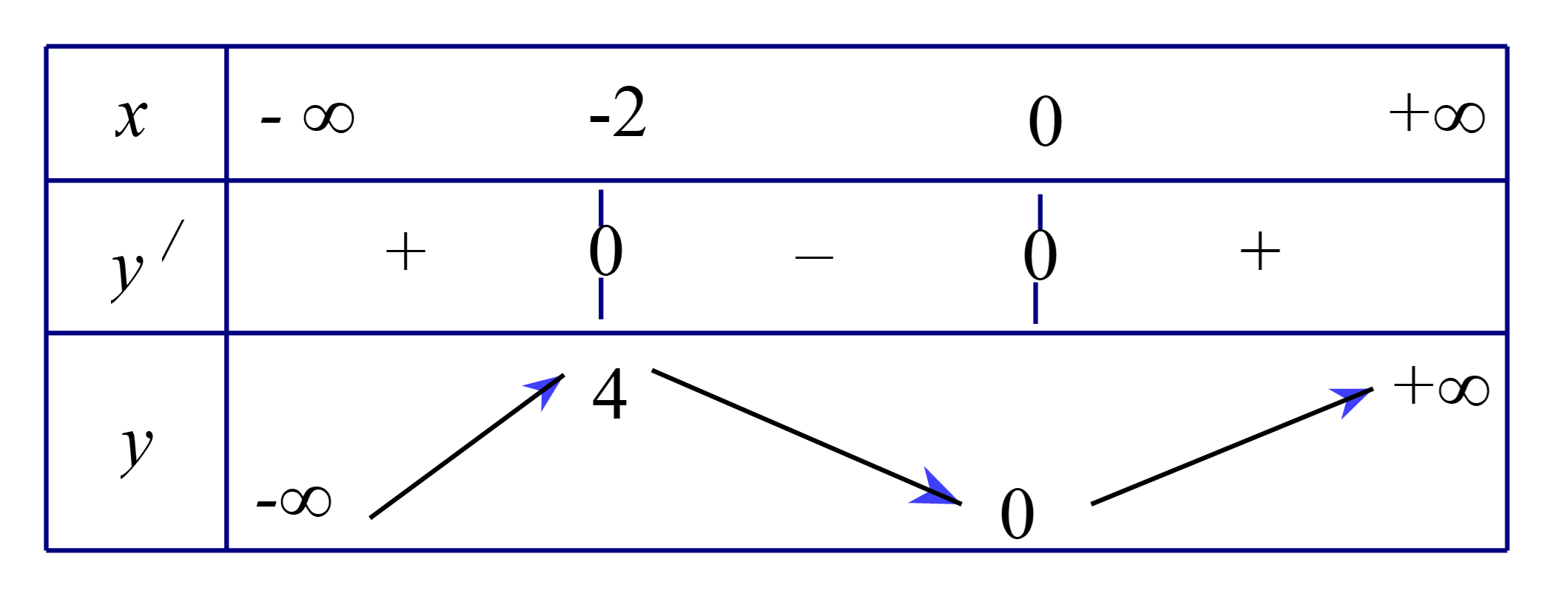
Cho hàm số f( x ) = x^3 + 3x^2 - m. Tìm các giá trị của m để đồ thị hàm số f( x ) cắt trục hoành tại 3 điểm phân biệt? A. [ m nhỏ hơn bằng 0; m lớn hơn bằng 4]. B. m thuộc [ 0;4] C. [m <
43
27/04/2024
Cho hàm số \[f\left( x \right) = {x^3} + 3{x^2} - m\]. Tìm các giá trị của m để đồ thị hàm số \[f\left( x \right)\] cắt trục hoành tại 3 điểm phân biệt?
A. \[\left[ \begin{array}{l}m \le 0\\m \ge 4\end{array} \right.\].
B. \(m \in \left[ {0;4} \right]\).
C. \[\left[ \begin{array}{l}m < 0\\m > 4\end{array} \right.\].
D. \[m \in \left( {0;4} \right)\].
Trả lời
Lời giải
Chọn D
Đồ hàm số \[y = f\left( x \right)\] cắt trục hoành tại 3 điểm phân biệt khi phương trình \[{x^3} + 3{x^2} = m\] có 3 nghiệm phân biệt.
Xét hàm số \[g\left( x \right) = {x^3} + 3{x^2}\]
TXĐ: \[D = \mathbb{R}\]
\[{g^/}\left( x \right) = 3{x^2} + 6x\];
\[{g^/}\left( x \right) = 0 \Leftrightarrow 3{x^2} + 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\]
Bảng biến thiên:
Dựa và BBT phương trình \[{x^3} + 3{x^2} = m\] có 3 nghiệm phân biệt khi \[m \in \left( {0;4} \right)\].
Chọn D
