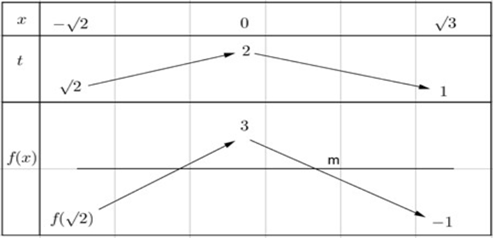
Cho hàm số f( x ) liên tục và tăng trên [ 1 ;2], f( 1 ) = - 1,f( 2 ) = 3. Có bao nhiêu số nguyên dương m để phương trình f( căn bậc hai của 4 - x^2) = m có nghiệm x thuộc [ - căn bậc hai của
Cho hàm số f(x) liên tục và tăng trên [1;2],f(1)=−1,f(2)=3. Có bao nhiêu số nguyên dương mđể phương trình f(√4−x2)=m có nghiệm x∈[−√2;√3) ?
A. 4.
B. 3.
C. 5.
D. 2.