Cho hàm số f( x ) có đạo hàm f'( x ) = x^2( x - 1)( x + 2)^3, x thuộc R. Số điểm cực trị của hàm số đã cho là A. 2 B. 1 C. 3. D. 5
Cho hàm số f(x) có đạo hàm f′(x)=x2(x−1)(x+2)3, ∀x∈R. Số điểm cực trị của hàm số đã cho là
A. 2.
B. 1.
C. 3.
D. 5.
Lời giải
Chọn A
f′(x)=0⇔[x=0x=1x=−2.
Ta có bảng xét dấu sau:
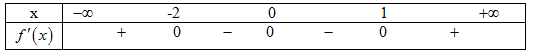
f′(x) đổi dấu khi qua x=−2 và f′(x)đổi dấu khi qua x=1 nên hàm số đã cho có 2 điểm cực trị.