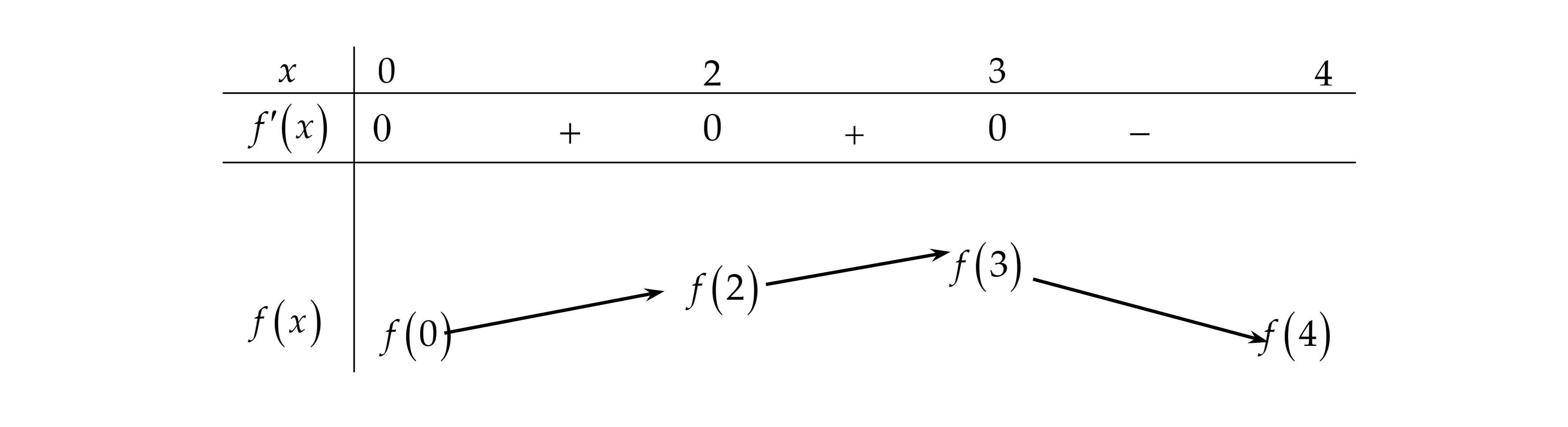Cho hàm số f( x ) có đạo hàm f'( x ) = - x( x - 2)^2( x - 3), x thuộc R. Giá trị lớn nhất của hàm số đã cho trên đoạn [ 0; 4] bằng A. f( 4 ). B. f( 0 ). C. f( 2 ). D.
Cho hàm số \(f\left( x \right)\)có đạo hàm \(f'\left( x \right) = - x{\left( {x - 2} \right)^2}\left( {x - 3} \right)\),\(\forall x \in \mathbb{R}\). Giá trị lớn nhất của hàm số đã cho trên đoạn \(\left[ {0\,;\,4} \right]\)bằng
A. \(f\left( 4 \right)\).
B. \(f\left( 0 \right)\).
C. \(f\left( 2 \right)\).
D. \(f\left( 3 \right)\).