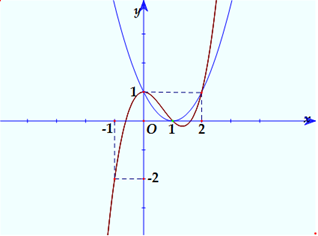
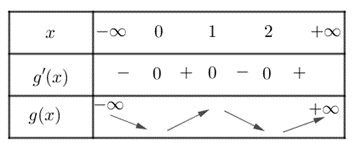
Cho hàm số f( x ) có đạo hàm f'( x ) có đồ thị như hình vẽ. Hàm số g( x ) = f( x ) - x^3/3 + x^2 - x + 2 đạt cực tiểu tại bao nhiêu điểm? A. 1. B. 2. C. 0. D. 3.
Cho hàm số \[f\left( x \right)\] có đạo hàm \[f'\left( x \right)\] có đồ thị như hình vẽ.
Hàm số \[g\left( x \right) = f\left( x \right) - \frac{{{x^3}}}{3} + {x^2} - x + 2\] đạt cực tiểu tại bao nhiêu điểm?
A. 1.
B. 2.
C. 0.
D. 3.