Cho hàm đa thức y = f( x ) có đồ thị hàm số y = f'( x ) như hình vẽ dưới đây. Số điểm cực trị của hàm số g( x ) = f( x^4 - 2x^2 - 3)
31
01/05/2024
Cho hàm đa thức \[y = f\left( x \right)\] có đồ thị hàm số \[y = f'\left( x \right)\] như hình vẽ dưới đây.
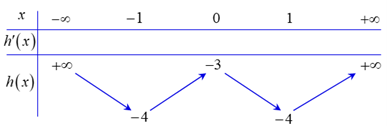
Số điểm cực trị của hàm số \[g\left( x \right) = f\left( {{x^4} - 2{x^2} - 3} \right) - 2{x^4} + 4{x^2} + 2020\] là
A. \(12\).
B. \(11\).
C. \(10\).
D. \(9\).
Trả lời
Lời giải
Chọn D
Ta có: \[g'\left( x \right) = \left( {4{x^3} - 4x} \right)f'\left( {{x^4} - 2{x^2} - 3} \right) - 8{x^3} + 8x = \left( {4{x^3} - 4x} \right)\left[ {f'\left( {{x^4} - 2{x^2} - 3} \right) - 2} \right]\]
\[ \Rightarrow g'\left( x \right) = 0\]\[ \Leftrightarrow \left[ \begin{array}{l}{x^3} - x = 0\\f'\left( {{x^4} - 2{x^2} - 3} \right) = 2\end{array} \right.\]
Theo đồ thị hàm số \[y = f'\left( x \right)\] ta có \[f'\left( x \right) = 2\].
Vậy \[g'\left( x \right) = 0\]
Xét hàm số \[h\left( x \right) = {x^4} - 2{x^2} - 3\] trên \[\mathbb{R}\].
Ta có \[h'\left( x \right) = 4{x^3} - 4x\], \[h'\left( x \right) = 0\]\[ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\end{array} \right.\], từ đó ta có BBT của \[y = h\left( x \right)\] như sau:
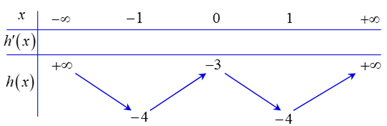
Từ BBT của hàm số \[h\left( x \right) = {x^4} - 2{x^2} - 3\], ta thấy \[h\left( x \right) = {x_1} \in \left( { - 4; - 3} \right)\] có đúng bốn nghiệm phân biệt. Vì vậy phương trình \[g'\left( x \right) = 0\] có đúng \[9\] nghiệm phân biệt là các nghiệm đơn và nghiệm bội lẻ nên hàm số \[y = g\left( x \right)\]có \[9\] điểm cực trị.


