Cho hai số phức $z,w$ thỏa mãn $\left|w+i\right|=\frac{3}{\sqrt{10}}$ và $10w=\left(3-i\right)\left(z-3\right)$. Giá trị lớn nhất của biểu thức $P=\left|z-2-i\right|+\left|z-6-i\right|$ bằng

Đáp án đúng là: D

Ta có: $10w=\left(3-i\right)\left(z-3\right)\iff 10\left(w+i\right)=\left(3-i\right)\left(z-3\right)+10i$.

Môđun hai vế ta được:

$\begin{array}{l}\left|10\left(w+i\right)\right|=\left|\left(3-i\right)\left(z-3\right)+10i\right|\iff 10\left|\left(w+i\right)\right|=\left|\left(3-i\right)\left[\left(z-3\right)+\frac{10i}{3-i}\right]\right|\\ \iff 10.\frac{3}{\sqrt{10}}=\left|\left(3-i\right)\left[\left(z-3\right)-1+3i\right]\right|\iff 3\sqrt{10}=\left|3-i\right|.\left|z-4+3i\right|\iff 3\sqrt{10}=\sqrt{10}.\left|z-4+3i\right|\\ \iff \left|z-4+3i\right|=3\end{array}$Đặt $z=x+yi\left(x,y\in ℝ\right)$ có điểm biểu diễn là $M\left(x;y\right)$.

Khi đó $\left|z-4+3i\right|=3\iff {\left(x-4\right)}^2+{\left(y+3\right)}^2=9$ nên tập hợp điểm biểu diễn số phức z là một đường tròn (C) có tâm I = (4;-3) và bán kính bằng R = 3.

Ta có $P=\left|z-2-i\right|+\left|z-6-i\right|=\left|z-\left(2+i\right)\right|+\left|z-\left(6+i\right)\right|=MA+MB$ với$A\left(2;1\right);B\left(6;1\right)$.

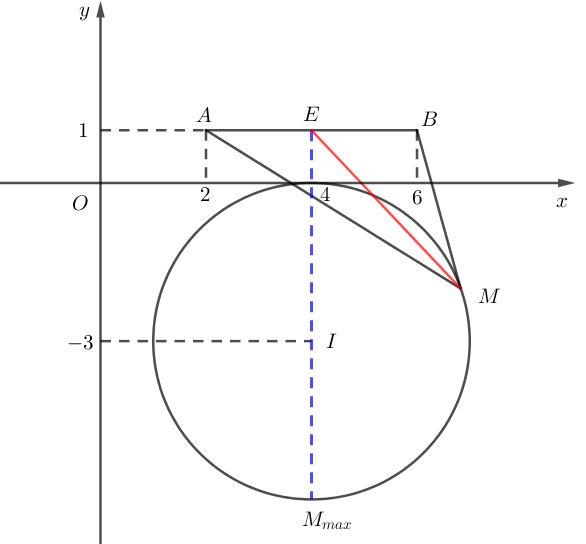
Gọi E là trung điểm của đoạn thẳng AB, suy ra E (4;1).

Xét tam giác MAB ta có:

 $M{E}^2=\frac{2\left(M{A}^2+M{B}^2\right)-A{B}^2}{4}\Rightarrow 2\left(M{A}^2+M{B}^2\right)=4M{E}^2+A{B}^2=4M{E}^2+16$.

Ta có:

$P^2={\left(MA+MB\right)}^2={\left(1.MA+1.MB\right)}^2\le \left(1^2+1^2\right)\left(M{A}^2+M{B}^2\right)$

$=2\left(M{A}^2+M{B}^2\right)=4M{E}^2+16$

$\Rightarrow P^2\le 4M{E}^2+16\le 4{\left(I{M}_{\max }+IE\right)}^2+16=4{\left(3+4\right)}^2+16=212\Rightarrow P\le \sqrt{212}=2\sqrt{53}$.