Cho đồ thị (C) của hàm số đa thức bậc ba và parabol (P) có đỉnh trên Ox và trục đối xứng của (P) vuông góc với trục hoành như hình

Cho đồ thị (C) của hàm số đa thức bậc ba và parabol (P) có đỉnh trên Ox và trục đối xứng của (P) vuông góc với trục hoành như hình vẽ. Tính diện tích của hình phẳng giới hạn bởi (C) và (P) (phần tô đen)

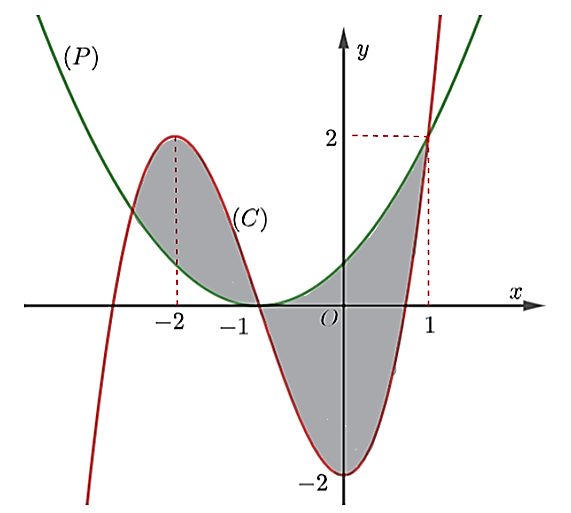
A. $\frac{3017}{192}$

B. $\frac{343}{192}$

C. $\frac{1393}{192}$

D. $\frac{937}{192}$

Trả lời

Đáp án đúng là: D

Xét $\left(P\right):\text{\hspace{0.17em}}f\left(x\right)=a{x}^2+bx+c$ có đỉnh $I\left(-1;0\right)$ và có $f(-1)=0;f\left(1\right)=2$

$\Rightarrow \left\{\begin{array}{l}-\frac{b}{2a}=-1\\ a-b+c=0\\ a+b+c=2\end{array}\right.\iff \left\{\begin{array}{l}a=\frac{1}{2}\\ b=1\\ c=\frac{1}{2}\end{array}\right.$

Vậy $\left(P\right):\text{\hspace{0.17em}}f\left(x\right)=\frac{1}{2}{x}^2+x+\frac{1}{2}$.

Xét $\left(C\right):g\left(x\right)=a{x}^3+b{x}^2+cx+d$$\Rightarrow g^{\text{'}}\left(x\right)=3a{x}^2+2bx+c$.

Ta có $\left\{\begin{array}{l}g\text{'}\left(-2\right)=0\\ g\text{'}\left(0\right)=0\\ g\left(0\right)=-2\\ g\left(1\right)=2\end{array}\right.\iff \left\{\begin{array}{l}12a-4b+c=0\\ c=0\\ d=-2\\ a+b+c+d=2\end{array}\right.\iff \left\{\begin{array}{l}a=1\\ b=3\\ c=0\\ d=-2\end{array}\right.$

Vậy $\left(C\right):g\left(x\right)=x^3+3x^2-2=0$

Phương trình hoành độ giao điểm

$x^3+3x^2-2=\frac{1}{2}{x}^2+x+\frac{1}{2}$$\iff x^3+\frac{5}{2}{x}^2-x-\frac{5}{2}=0\iff x=\frac{-5}{2};x=-1;x=1$.

Diện tích hình phẳng giới hạn bởi (C)và (P) là:

$S=\underset{-\frac{5}{2}}{\overset{1}{\int }}\left|\left(x^3+3x^2-2\right)-\left(\frac{1}{2}{x}^2+x+\frac{1}{2}\right)\right|\text{\hspace{0.17em}d}x$

$=\underset{-\frac{5}{2}}{\overset{1}{\int }}\left|x^3+\frac{5}{2}{x}^2-x-\frac{5}{2}\right|\text{\hspace{0.17em}d}x$$=\underset{-\frac{5}{2}}{\overset{-1}{\int }}\left|x^3+\frac{5}{2}{x}^2-x-\frac{5}{2}\right|\text{\hspace{0.17em}d}x+\underset{-1}{\overset{1}{\int }}\left|x^3+\frac{5}{2}{x}^2-x-\frac{5}{2}\right|\text{\hspace{0.17em}d}x$

$=\underset{-\frac{5}{2}}{\overset{-1}{\int }}\left(x^3+\frac{5}{2}{x}^2-x-\frac{5}{2}\right)\text{\hspace{0.17em}d}x+\underset{-1}{\overset{1}{\int }}\left(-x^3-\frac{5}{2}{x}^2+x+\frac{5}{2}\right)\text{\hspace{0.17em}d}x$

$=\frac{99}{64}+\frac{10}{3}=\frac{937}{192}$.