Cho điểm M(x0; y0) và đường thẳng ∆: ax + by + c = 0 có vectơ pháp tuyến . Gọi H là hình chiếu vuông góc của M

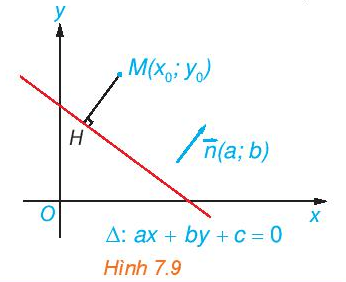
HĐ4 trang 40 Toán 10 Tập 2: Cho điểm M(x₀; y₀) và đường thẳng ∆: ax + by + c = 0 có vectơ pháp tuyến $\overrightarrow{n}\left(a;b\right)$. Gọi H là hình chiếu vuông góc của M trên ∆ (H.7.9). 

a) Chứng minh rằng $\left|\overrightarrow{n}.\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$.

b) Giả sử H có tọa độ (x₁; y₁). Chứng minh rằng: $\overrightarrow{n}.\overrightarrow{HM}$= a(x₀ – x₁) + b(y₀ – y₁) = ax₀ + by₀ + c. 

c) Chứng minh rằng $HM=\frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}$. 

Trả lời

a) Do H là hình chiếu của M lên ∆ nên MH ⊥ ∆.

Vectơ $\overrightarrow{n}$ là vectơ pháp tuyến của ∆ nên giá của vectơ $\overrightarrow{n}$ vuông góc với ∆. 

Khi đó đường thẳng MH song song hoặc trùng với giá của vectơ $\overrightarrow{n}$ nên hai vectơ $\overrightarrow{HM}$ và $\overrightarrow{n}$cùng phương. 

Do đó hai vectơ $\overrightarrow{HM}$ và $\overrightarrow{n}$ cùng hướng hoặc ngược hướng.

+) Nếu hai vectơ $\overrightarrow{HM}$ và $\overrightarrow{n}$ cùng hướng thì $\overrightarrow{n}.\overrightarrow{HM}=\left|\overrightarrow{n}\right|.\left|\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$.

+) Nếu hai vectơ $\overrightarrow{HM}$ và $\overrightarrow{n}$ ngược hướng thì $\overrightarrow{n}.\overrightarrow{HM}=-\left|\overrightarrow{n}\right|.\left|\overrightarrow{HM}\right|=-\sqrt{a^2+b^2}.HM$.

Vậy $\left|\overrightarrow{n}.\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$. 

b) Vì H thuộc ∆ nên tọa độ của H thỏa mãn phương trình ∆, thay tọa độ của H vào phương trình ∆ ta được: ax₁ + by₁ + c = 0 ⇔ c = – ax₁ – by₁           (1). 

Ta lại có: $\overrightarrow{HM}=\left(x_0-x_1;y_0-y_1\right)$.

Suy ra: $\overrightarrow{n}.\overrightarrow{HM}=a\left(x_0-x_1\right)+b\left(y_0-y_1\right)$ = ax₀ + by₀ – ax₁ – by₁             (2). 

Từ (1) và (2) suy ra : $\overrightarrow{n}.\overrightarrow{HM}=a\left(x_0-x_1\right)+b\left(y_0-y_1\right)$ = ax₀ + by₀ + c. 

c) Theo câu a) ta có: $\left|\overrightarrow{n}.\overrightarrow{HM}\right|=\sqrt{a^2+b^2}.HM$. 

Theo câu b) ta có: $\overrightarrow{n}.\overrightarrow{HM}$ = ax₀ + by₀ + c. 

Suy ra: |ax₀ + by₀ + c| = $\sqrt{a^2+b^2}.HM$.

Vậy $HM=\frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}$.