Cho AB và CD là hai dây cung vuông góc tại E của đường tròn (O). Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ để chứng minh EF
389
13/06/2023
Bài 2 trang 73 Toán lớp 10 Tập 2: Cho AB và CD là hai dây cung vuông góc tại E của đường tròn (O). Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ để chứng minh EF vuông góc với DB.
Trả lời
Ta có hình vẽ sau:
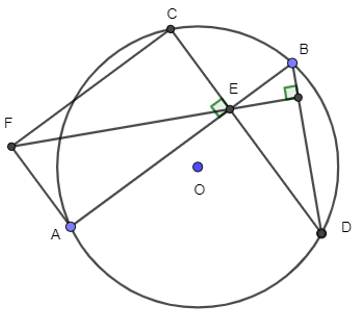
Đặt AE = a, EB = b, EC = c, ED = d.
Ta chọn hệ trục tọa độ sao cho E(0; 0), A(a; 0), B(b; 0), C(0; c) và D(0; d) và F(a; c).
Xét ∆AEC và ∆DEB, có:
^AEC=^DEB=90°
(hai góc nội tiếp cùng chắn )
⇒ ∆AEC ∽ ∆DEB (g – g)
⇒
⇒
⇔ AE.EB = DE.EC
⇔ AE.EB = DE.EC
⇔ a.b = d.c
⇔ d.c – ab = 0
Ta có: = (a; c), = (-b; d)
⇒ = a.(-b) + c.d = - ab + cd = 0
⇒
⇒ EF ⊥ BD.
Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Đường tròn trong mặt phẳng toạ độ
Bài 4: Ba đường conic trong mặt phẳng tọa độ
Bài tập cuối chương 9
Bài 1: Không gian mẫu và biến cố
Bài 2: Xác suất của biến cố
Bài tập cuối chương 10

