Cắt một khối nón bởi mặt phẳng đi qua trục của nó, ta được một tam giác vuông cân có diện tích bằng 8. Khẳng định nào sau đây sai ?

D. Khối nón có thể tích bằng $\frac{{16\pi \sqrt 2 }}{3}$

Phương pháp:

Diện tích hình tròn bán kính R: $S = \pi {R^2}$

Diện tích xung quanh của khối nón: ${S_{xq}} = \pi Rl$

Cách giải:

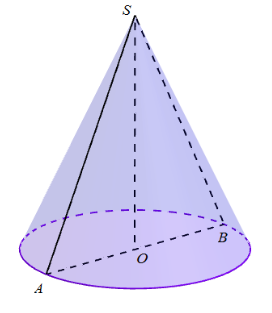
Theo đề bài, ta có tam giác SAB vuông cân tại S và ${S_{\Delta SAB}} = 8$

Ta có: ${S_{\Delta SAB}} = \frac{1}{2}.SO.AB = \frac{1}{2}.OA.2OA = O{A^2} = 8 \Rightarrow OA = 2\sqrt 2$

$\Rightarrow$ Đường tròn đáy có bán kính $R = OA = 2\sqrt 2$

Diện tích đáy: $S = \pi {R^2} = \pi {\left( {2\sqrt 2 } \right)^2} = 8\pi$

Độ dài đường sinh: $l = SA = OA.\sqrt 2 = 2\sqrt 2 .\sqrt 2 = 4$

Diện tích xung quanh của khối nón: ${S_{xq}} = \pi Rl = \pi .2\sqrt 2 .4 = 8\sqrt 2 \pi$

Đường cao: $h = SO = OA = 2\sqrt 2$

Thể tích khối nón: $V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi .{\left( {2\sqrt 2 } \right)^2}.2\sqrt 2 = \frac{{16\sqrt 2 \pi }}{3}$