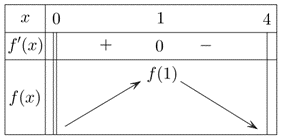
Biết rằng hàm số f( x ) = - x + 2018 - 1/x đạt giá trị lớn nhất trên khoảng ( 0;4) tại x0. Tính P = x0 + 2018 A. P = 4032 B. P = 2020 C. P = 2018 D. P = 2019
Biết rằng hàm số f(x)=−x+2018−1x đạt giá trị lớn nhất trên khoảng (0;4) tại x0. Tính P=x0+2018.
A. P=4032.
B. P=2020.
C. P=2018.
D. P=2019.