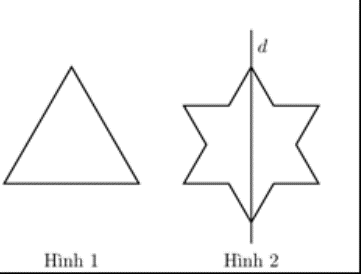
Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác
20
01/05/2024
Ban đầu ta có một tam giác đều cạnh bằng 3 (hình 1). Tiếp đó ta chia mỗi cạnh của tam giác thành 3 đoạn bằng nhau và thay mỗi đoạn ở giữa bởi hai đoạn bằng nó sao cho chúng tạo với đoạn bỏ đi một tam giác đều về phía ngoài ta được hình 2. Khi quay hình 2 xung quanh trục d ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
A. \(\frac{{5\pi \sqrt 3 }}{3}\)
B. \(\frac{{9\pi \sqrt 3 }}{3}\)
C. \(\frac{{7\pi \sqrt 3 }}{3}\)
D. \(\frac{{5\pi \sqrt 3 }}{2}\)
Trả lời
Đáp án C
Phương pháp:
Sử dụng các công thức tính thể tích khối trụ, khối nón.
Cách giải:
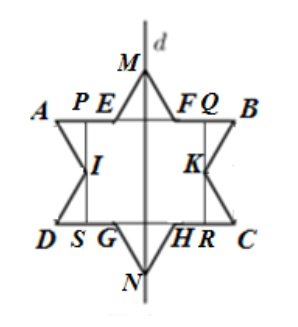
Kẻ PS, QR lần lượt qua I và K và vuông góc với AB.
Dễ thấy P, Q, R, S lần lượt là trung điểm của AE, BF, CH, DG.
Hình chữ nhật PQRS có \(PQ = \frac{1}{2} + 1 + \frac{1}{2} = 2,\,\,QK = \frac{{\sqrt 3 }}{2} \Rightarrow QR = \sqrt 3 \)
Quay hình chữ nhật PQRS quanh d ta được \({V_1} = \pi {\left( {\frac{{PQ}}{2}} \right)^2}QR = \pi {.1^2}.\sqrt 3 = \sqrt 3 \pi \)
Khi quay tam giác MEF quanh d ta được \({V_2} = \frac{1}{3}\pi .{\left( {\frac{1}{2}} \right)^2}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 \pi }}{{24}}\)
Tương tự khi quay tam giác NGH quanh d ta được khối tròn xoay có thể tích \({V_2}\)
Xét tam giác vuông API có: \(PI = \frac{{\sqrt 3 }}{2}\)
Khi quay tam giác API quanh d ta được \({V_3} = \frac{1}{3}\pi .A{P^2}.PI = \frac{1}{3}\pi {\left( {\frac{1}{2}} \right)^2}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 \pi }}{{24}}\)
Vậy khi xoay hình đã cho quanh d ta được vật tròn xoay có thể tích:
\(V = {V_1} + 2{V_2} + 4.\frac{{{V_3}}}{1} = \frac{{7\sqrt 3 \pi }}{6}\)