Dạng 3: Biến đổi, rút gọn biểu thức đại số có chứa phép nhân đa thức
-
129 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Rút gọn biểu thức (2x – 3y)(3x + 5y)(x – 7y) ta được
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Ta có: (2x – 3y)(3x + 5y)(x – 7y)
= [(2x – 3y)(3x + 5y)](x – 7y)
= (6x2 + 10xy – 9xy – 15y2)(x – 7y)
= (6x2 + xy – 15y2)(x – 7y)
= 6x3 – 42x2y + x2y – 7xy2 – 15xy2 + 105y3
= 6x3 – 41x2y – 22xy2 + 105y3.
Câu 2:
Giá trị biểu thức A = (– x2y + 2xy)(– 3x3y) tại x = – 1 và y = 2 là
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Rút gọn biểu thức:
(– x2y + 2xy)(– 3x3y)
= – x2y(– 3x3y) + 2xy(– 3x3y)
= 3x5y2 – 6x4y2
Thay x = – 1 và y = 2 vào biểu thức vừa thu gọn, ta được:
A = 3.(–1)5.22 – 6.(–1)4.22 = 3.(–1).4 – 6.1.4 = – 12 – 24 = – 36.
Vậy giá trị của biểu thức A tại x = – 1 và y = 2 là – 36.
Câu 3:
Khu vườn trồng mía của nhà bác Minh ban đầu có dạng một hình vuông biết chu vi hình vuông là 20 (m) sau đó được mở rộng bên phải thêm y (m), phía dưới thêm 8x (m) nên mảnh vườn trở thành một hình chữ nhật (hình vẽ).
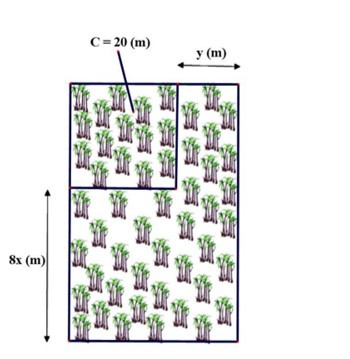
Diện tích khu vườn nhà bác Minh sau khi được mở rộng với x = 1; y = 2 là bao nhiêu mét vuông?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Vì chu vi của hình vuông là 20 m nên mỗi cạnh sẽ có độ dài là 20 : 4 = 5 m.
Khi khu vườn được mở rộng, nó trở thành một hình chữ nhật với hai kích thước lần lượt là 5 + y (m) và 5 + 8x (m).
Do đó diện tích của khu vườn hình chữ nhật là:
(5 + y).(5 + 8x) = 25 + 40x + 5y + 8xy (m2).
Diện tích khu vườn nhà bác Minh sau khi được mở rộng với x = 1; y = 2 là:
25 + 40.1 + 5.2 + 8.1.2 = 25 + 40 + 10 + 16 = 91 (m2).
Vậy diện tích khu vườn nhà bác Minh sau khi được mở rộng là 91 (m2).
Câu 4:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Ta có:
(15ab + 1)(a2b – 3ab + 5)
= 15ab(a2b – 3ab + 5) + 1.(a2b – 3ab + 5)
= 15a3b2 – 45a2b2 + 75ab + a2b – 3ab + 5
= 15a3b2 – 45a2b2 + a2b + 72ab + 5.
Hạng tử bậc 5 là 15a3b2;
Hạng tử bậc 4 là – 45a2b2;
Hạng tử bậc hai là 72ab.
Vậy tổng các hệ số của lũy thừa bậc năm, lũy thừa bậc bốn và lũy thừa bậc hai trong kết quả của phép nhân là 15 + (– 45) + 72 = 42.
Câu 5:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
P = x(x – y + 1) – y(x + y – 1)
= x2 – xy + x – xy – y2 + y
= x2 – xy + x + xy – y2 + y
= x2 + x + y – y2.
Vậy P = x2 + x + y – y2.
Câu 6:
Cho biểu thức P = x(y + z – yz) – y(z + x – zx) + z(y – x). Chọn khẳng định đúng.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Ta có:
P = x(y + z – yz) – y(z + x – zx) + z(y – x)
P = xy + xz – xyz – yz – xy + xyz + yz – xz
P = 0.
Do đó P không phụ thuộc vào x, y và z.
Câu 7:
Cho biểu thức M = (5x – y)(5x + y) – (5x + 2y)(5x – 2y) + 10 + 3y2. Nhận định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Ta có:
M = (5x – y)(5x + y) – (5x + 2y)(5x – 2y) + 10 + 3y2
= 5x(5x + y) – y(5x + y) – [5x(5x – 2y) + 2y(5x – 2y)] + 10 + 3y2
= 25x2 + 5xy – 5xy – y2 – [25x2 – 10xy + 10xy – 4y2] + 10 + 3y2
= 25x2 – y2 – (25x2 – 4y2) + 10 + 3y2
= 25x2 – y2 – 25x2 + 4y2 + 10 + 3y2
= (25x2 – 25x2) + (– y2 + 4y2 + 3y2) + 10
= 6y2 + 10.
Biểu thức trên không phụ thuộc vào biến x.
Câu 8:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Ta có:
2(x + 1)(y + 1)
= 2(xy + x + y + 1)
= 2xy + 2x + 2y + 2.
(x + y)(x + y + 2)
= x(x + y + 2) + y(x + y + 2)
= x2 + xy + 2x + xy + y2 + 2y
= (x2 + y2) + 2xy + 2x + 2y
= 2 + 2xy + 2x + 2y (do x2 + y2 = 2).
Do đó 2(x + 1)(y + 1) = (x + y)(x + y + 2).
Vậy ta chọn phương án B.
Câu 9:
Cho các đẳng thức sau:
Với a2 + b2 + c2 = 0 thì
(I) a2(a2 + b2)(a2 + c2) = b2(a2 + b2)(b2 + c2);
(II) a2(a2 + b2)(a2 + c2) = c2(a2 + c2)(b2 + c2);
(III) c2(a2 + c2)(b2 + c2) = b2(a2 + b2)(b2 + c2);
Khẳng định nào sau đây là đúng nhất?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Ta có: a2 + b2 + c2 = 0 nên ta có:
⦁ a2 + b2 = –c2;
⦁ b2 + c2 = –a2;
⦁ c2 + a2 = –b2.
Do đó a2(a2 + b2)(a2 + c2) = a2.(–c2).(–b2) = a2b2c2;
b2(a2 + b2)(b2 + c2) = b2.(–c2).(–a2) = a2b2c2;
c2(a2 + c2)(b2 + c2) = c2.(–b2).(–a2) = a2b2c2.
Khi đó a2(a2 + b2)(a2 + c2) = b2(a2 + b2)(b2 + c2) = c2(a2 + c2)(b2 + c2).
Vậy cả (I), (II) và (III) đều đúng.
Câu 10:
Cho các số x, y, z lần lượt tỉ lệ với các số a, b, c khác 0. Khi đó (x2 + 2y2 + 3z2)(a2 + 2b2 + 3c2) bằng
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Do x, y, z lần lượt tỉ lệ với các số a, b, c khác 0 nên ta có
Suy ra x = ka; y = kb; z = kc.
Ta có:
(x2 + 2y2 + 3z2)(a2 + 2b2 + 3c2)
= (k2a2 + 2k2b2 + 3k2c2)(a2 + 2b2 + 3c2)
= k2(a2 + 2b2 + 3c2)(a2 + 2b2 + 3c2)
= k2(a2 + 2b2 + 3c2)2
= [k(a2 + 2b2 + 3c2)]2
= (k.a2 + k.2b2 + k.3c2)2
= (ax + 2by + 3cz)2 (do x = ka; y = kb; z = kc).
Vậy ta chọn phương án B.