Trắc nghiệm Toán 7 KNTT Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác có đáp án
Dạng 2: Tìm và chứng minh hai tam giác bằng nhau theo trường hợp cạnh - cạnh - cạnh từ đó chứng minh tính chất khác có đáp án
-
210 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho hình vẽ bên dưới:
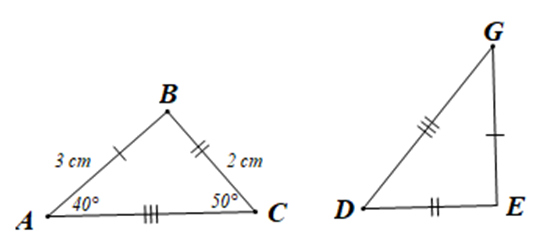
Số đo góc DGE và độ dài cạnh EG lần lượt là:
Xem đáp án
Đáp án đúng là: C
Xét tam giác ABC và tam giác DEG có:
AB = GE, BC = ED, AC = GD (giả thiết)
Suy ra DABC = DGED (c.c.c)
Do đó EG = BA = 3 cm (hai cạnh tương ứng) và ^DGE=^CAB=40∘ (hai góc tương ứng)
Vậy ^DGE=40∘, EG = 3 cm.
Câu 2:
Cho hai tam giác ABC và OHK có AB = OH, AC = HK. Điều kiện để DABC = DHOK theo trường hợp cạnh – cạnh – cạnh là:
Xem đáp án
Đáp án đúng là: A
Vì DABC = DHOK theo trường hợp cạnh – cạnh – cạnh mà AB = OH, AC = HK
Nên điều kiện còn thiếu là BC = OK.
Câu 3:
Cho hình vẽ dưới đây:
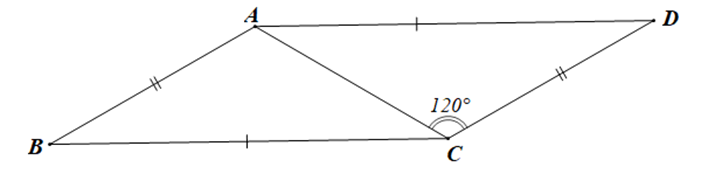
Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: D
Xét tam giác ABC và tam giác ACD có:
AB = CD, BC = DA, AC là cạnh chung
Suy ra DABC = DCDA (c.c.c)
Do đó ^BAC=^DCA (hai góc tương ứng)
Mà ^DCA=120∘
Nên ^BAC=120∘
Mặt khác: DABC = DCDA (chứng minh trên)
Suy ra ^DAC=^BCA (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong
Do đó AD // BC (dấu hiệu nhận biết)
Vậy ^BAC=120∘ và AD // BC.
Câu 4:
Cho hình dưới đây:
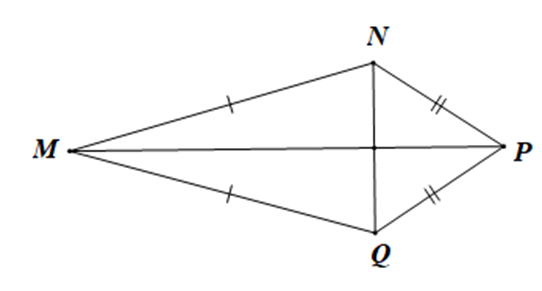
Xét các khẳng định:
(1) MP là tia phân giác của ^NMQ;
(2) NQ là tia phân giác của ^MNP.
Chọn khẳng định đúng:
Xem đáp án
Đáp án đúng là: A
+ Xét tam giác MNP và tam giác MPQ có:
MN = MQ, NP = QP, MP là cạnh chung
Suy ra DMNP = DMQP (c.c.c)
Do đó ^NMP=^QMP (hai góc tương ứng)
Nên MP là tia phân giác của ^NMQ. Do đó (1) là đúng.
+ Xét khẳng định (2): NQ là tia phân giác của ^MNP.
Để NQ là tia phân giác của ^MNP thì ^MNQ=^QNP nhưng không có dữ kiện nào để khẳng định điều này.
Vậy chỉ có (1) đúng.
Câu 5:
Xét bài toán “DOAB và DOAC có AB = AC, OB = OC (điểm O nằm ngoài tam giác ABC). Chứng minh rằng ^OAB=^OAC.”
Cho các câu sau:
(1) Suy ra DOAB = DOAC (c.c.c);
(2) AB = AC (giả thiết),
OB = OC (giả thiết),
OA là cạnh chung;
(3) Do đó ^OAB=^OAC (hai góc tương ứng).
(4) Xét DOAB và DOAC có:
Hãy sắp xếp một cách hợp lí các câu trên để giải bài toán.
Xem đáp án
Đáp án đúng là: B
Ta đi chứng minh ^OAB=^OAC như sau:
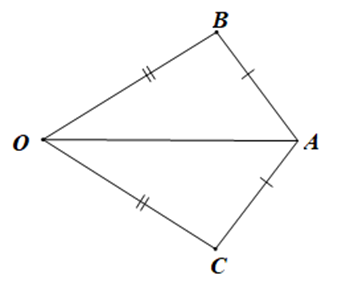
Xét DOAB và DOAC có:
AB = AC (giả thiết),
OB = OC (giả thiết),
OA là cạnh chung;
Suy ra DOAB = DOAC (c.c.c);
Do đó ^OAB=^OAC (hai góc tương ứng).
Vậy ta chọn phương án B.
Câu 6:
Cho hình vẽ dưới đây:
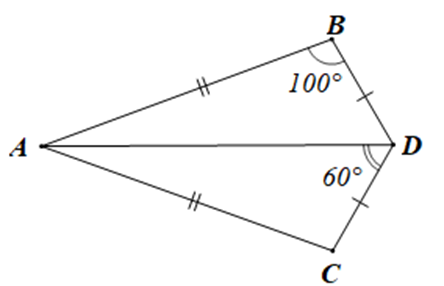
Số đo của ^BAC trong hình vẽ trên bằng:
Xem đáp án
Đáp án đúng là: B
Xét tam giác ABD và tam giác ACD có:
AB = AC, BD = CD, AD là cạnh chung
Suy ra DABD = DACD (c.c.c)
Do đó ^BAD=^CAD,ˆB=ˆC,^BDA=^CDA (các cặp cạnh tương ứng)
Nên ^BDA=^CDA=60∘
Xét tam giác ABD có: ^BAD+ˆB+^BDA=180∘ (tổng ba góc trong một tam giác)
Suy ra \[\widehat {BAD} = 180^\circ - \widehat B - \widehat {BDA}\]
Hay ^BAD=180∘−100∘−60∘=20∘
Mà ^BAD=^CAD nên ^BAD=^CAD=20∘
Mặt khác ^BAC=^BAD+^CAD=20∘+20∘=40∘
Vậy số đo của ^BAC bằng 40°.
Câu 7:
Trên hình vẽ dưới đây:
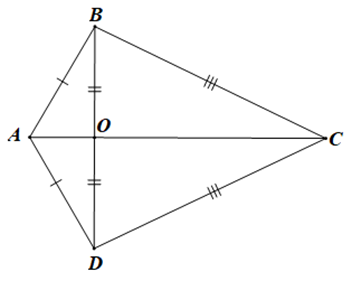
Số cặp tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh là:
Xem đáp án
Đáp án đúng là: C
+) Xét tam giác ABC và tam giác ADC có:
AB = AD, BC = DC, AC là cạnh chung
Suy ra DABC = DADC (c.c.c)
+) Xét tam giác ABO và tam giác ADO có:
AB = AD, BO = DO, AO là cạnh chung
Suy ra DABO = DADO (c.c.c)
+) Xét tam giác CBO và tam giác CDO có:
CB = CD, BO = DO, CO là cạnh chung
Suy ra DCBO = DCDO (c.c.c)
Vậy trong hình vẽ trên có 3 cặp tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh.
Câu 8:
Cho tam giác ABC có AB = AC, M là trung điểm của BC. Biết ^ABC=40∘, số đo của ^BAM là:
Xem đáp án
Đáp án đúng là: D
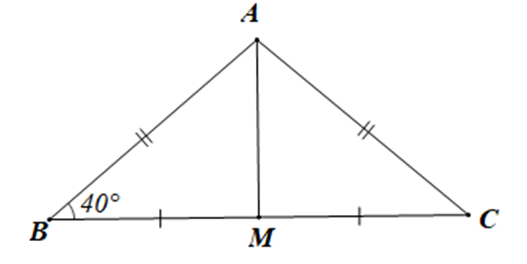
Xét tam giác ABM và tam giác ACM có:
AB = AC (giả thiết),
MB = MC (do M là trung điểm của BC),
AM là cạnh chung
Do đó DABM = DACM (c.c.c)
Suy ra ^BAM=^CAM,^AMB=^AMC (các cặp góc tương ứng)
Mà ^AMB+^AMC=180∘ (hai góc kề bù)
Nên ^AMB=^AMC=180∘2=90∘
Do đó tam giác ABM vuông tại M
Khi đó ^ABM+^BAM=90∘ (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra ^BAM=90∘−^ABM=90∘−40∘=50∘.
Vậy ta chọn phương án D.
Câu 9:
Cho tam giác ABC (AB < AC). Trên cạnh AC lấy điểm D sao cho AB = AD. Lấy M là trung điểm của BC. Qua C kẻ đường thẳng vuông góc với BD tại N. Chọn khẳng định sai:
Xem đáp án
Đáp án đúng là: C
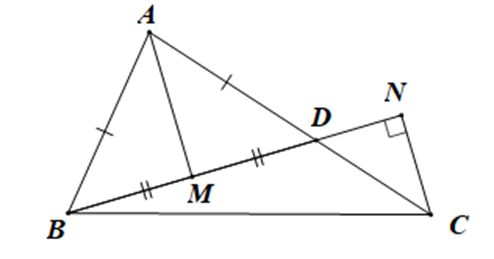
Xét tam giác ABM và tam giác ADM có:
AB = AD (giả thiết),
MB = MD (do M là trung điểm của BD),
AM là cạnh chung
Suy ra DABM = DADM (c.c.c)
Do đó ^BAM=^DAM,^AMB=^AMD (các cặp góc tương ứng)
Mà ^AMB+^AMD=180∘ (hai góc kề bù)
Nên ^AMB=^AMD=180∘2=90∘
Do đó AM ^ BD.
Mà CN ^ BD (giả thiết), nên AM // CN.
Suy ra ^DAM=^ACN (hai góc so le trong)
Lại có ^BAM=^DAM (chứng minh trên)
Khi đó ^BAM=^ACN.
Vậy ta chọn phương án C.
Câu 10:
Cho tam giác ABC, vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm B bán kính AC, hai dây cung này cắt nhau tại D (D và C nằm khác phía so với đường thẳng AB). Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: C
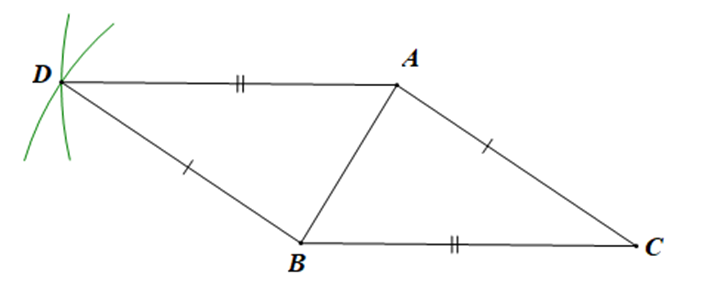
Xét tam giác ABC và tam giác ABD có:
AD = BC (D nằm trên cung tròn tâm A bán kính BC),
AC = BD (D nằm trên cung tròn tâm B bán kính AC),
AB là cạnh chung
Do đó DABC = DBAD (c.c.c)
Suy ra ^ABC=^BAD,^BAC=^ABD (các cặp góc tương ứng)
Mà ^ABC và ^BAD ở vị trí so le trong của AD và BC nên AD // BC (dấu hiệu nhận biết)
^BAC và ^ABD ở vị trí so le trong của AC và BD nên AC // BD (dấu hiệu nhận biết)
Vậy ta chọn phương án C.