25 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Đạo hàm cơ bản (P3)

Câu 1:

Cho hàm số . Tập nghiệm của phương trình f’(x) = 0 là

Xem đáp án

Chọn C.

Ta có

Câu 2:

Tìm số f(x) = x³ – 3x² + 1. Đạo hàm của hàm số f(x) âm khi và chỉ khi.

A. 0 < x < 2.

B. x < 1.

C. x < 0 hoặc x > 1

D. x < 0 hoặc x > 2.

Xem đáp án

Chọn A.

Ta có: f’(x) = 3x² – 6x.

f’(x) < 0 ⇔ 3x² – 6x < 0 ⇔ 0 < x < 2.

Câu 3:

Cho hàm số . Để y’ > 0 thì x nhận các giá trị thuộc tập nào sau đây?

A. (-∞; +∞).

D. ∅.

Xem đáp án

Chọn C.

Câu 4:

Cho hàm số y = (2x² + 1)³. Để y’ ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây?

A. ∅.

B. (-∞; 0].

C. [0; +∞).

D. R

Xem đáp án

Chọn C.

Ta có: y = (2x² + 1)³ ⇒ y’ = 12x(2x² + 1)² ⇒ y’ ≥ 0 ⇔ x ≥ 0.

Câu 5:

Cho hàm số . Để y’ ≤ 0 thì x nhận các giá trị thuộc tập nào sau đây?

A. ∅.

B. (-∞; 0).

C. (0; +∞).

D. (-∞; 0].

Xem đáp án

Chọn D.

Tập xác định: D = R.

( vì với mọi x thì $4 x^{2} + 1 > 0$ )

Câu 6:

Cho hàm số 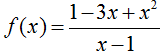. Tập nghiệm của bất phương trình f’(x) > 0 là

A. R \ {1}.

B. ∅.

C. (1; +∞).

D. R.

Xem đáp án

Chọn D.

Vì ${(x - 1)}^{2} + 1 > 0; {(x - 1)}^{2} > 0 \forall x \neq 1$

Do đó, tập nghiệm của bất phương trình f'(x) > 0 là R.

Câu 7:

Cho hàm số y = x³. Viết tiếp tuyến của đồ thị hàm số đã cho. Biết tiếp điểm là M(1; 1).

A: y = 3x + 1

B: y = 3x - 1

C: y = 3x + 2

D: y = 3x - 2

Xem đáp án

Chọn D.

Đặt f(x) = x³ ⇒ f’(x) = 3x²

Gọi k là hệ số góc của tiếp tuyến tại M

k = f’(1) = 3.

⇒ PTTT tại M là: y = 3(x - 1) + 1 hay y = 3x - 2.

Câu 8:

Cho hàm số y = x³. Viết tiếp tuyến của đồ thị hàm số đã cho. Biết hoành độ tiếp điểm bằng 2.

A: y = 12x + 1

B: y = 12x - 16

C: y = 6x + 2

D: y = 6x - 12

Xem đáp án

Chọn B.

Gọi M(x_M; y_M) là tiếp điểm. Theo giả thiết:

Đặt f(x) = x³ ⇒ f’(x) = 3x²

Gọi k là hệ số góc của tiếp tuyến tại M ⇒ k = f’(2) = 12

⇒ PTTT tại M là: y = 12(x – 2) + 8

Hay y = 12x - 16.

Câu 9:

Cho hàm số 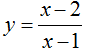. Viết PTTT của đồ thị hàm số biết . Tiếp điểm M có tung độ bằng 4

A: y = 9x + 2

B: y = 9x - 16

C: y = 9x + 8

D: y = 9x - 2

Xem đáp án

Chọn D.

Đặt

Gọi M(x_M; y_M) là tiếp điểm.

Theo gt:

Gọi k là hệ số góc của TT tại

⇒ PTTT tại M là:

Câu 10:

Cho hàm số 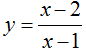. Viết PTTT của đồ thị hàm số biết. Tiếp điểm M là giao điểm của đồ thị hàm số với trục tung

A: y = 2x + 1

B: y = 2x - 6

C: y = x + 2

D: y = x - 12

Xem đáp án

Chọn C.

Ta có:

Gọi M(x_M; y_M) là tiếp điểm

Theo gt:

Gọi k là hệ số của tt tại M ⇒ k = f’(0) = 1.

PTTT tại M là y =1. (x - 0) + 2 hay y = x + 2.

Câu 11:

Cho hàm số y = x³ + x² + x + 1. Viết PTT tại M thuộc đồ thị hàm số biết tung độ điểm M bằng 1.

A: y = 2x + 1

B: y = x + 1

C: y = x + 2

D: y = x - 1

Xem đáp án

Chọn B.

Đặt f(x) = x³ + x² + x + 1 ⇒ f’(x) = (x³ + x² + x + 1)’ = 3x² + 2x + 1

Gọi M(x_M; y_M) là tiếp điểm

Theo gt:

Gọi k là hệ số góc của tiếp tuyến tại M; k = f’(0) = 3.0+ 2.0+ 1 = 1

⇒ Pttt tại M có tung độ bằng 1 là: y = 1. (x – 0) + 1

Hay y = x + 1.

Câu 12:

Cho hàm số 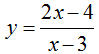có đồ thị là (H). Phương trình tiếp tuyến tại giao điểm của (H) với trục hoành là:

A. y = 2x – 4.

B. y = 3x + 1.

C. y = - 2x + 4.

D. y = 2x.

Xem đáp án

Chọn C.

Phương trình hoành độ giao điểm của đồ thị với trục hoành:

$\frac{2 x - 4}{x - 3} = 0 \Leftrightarrow 2 x - 4 = 0 \Leftrightarrow x = 2$

Giao điểm của (H) với trục hoành là A(2; 0).

Ta có:

Phương trình tiếp tuyến cần tìm là y = -2(x - 2) hay y = -2x + 4.

Câu 13:

Phương trình tiếp tuyến của đồ thị hàm số f(x) = x³ – 2x² + 3x tại điểm có hoành độ x_o = -1 là:

A. y = 10x + 4.

B. y = 10x – 5.

C. y = 2x – 4.

D. y = 2x – 5.

Xem đáp án

Chọn A.

Đạo hàm: y’ = 3x² – 4x + 3.

y'(-1) = 10; y(-1) = -6

Phương trình tiếp tuyến cần tìm là (d): y = 10(x + 1) – 6 = 10x + 4.

Câu 14:

Trong các tiếp tuyến tại các điểm trên đồ thị hàm số y = x³ – 3x² + 2, tiếp tuyến có hệ số góc nhỏ nhất bằng

A. -3

B. 3

C. 4

D. 0

Xem đáp án

Chọn A.

Đạo hàm: y’ = 3x² – 6x = 3(x – 1)² – 3 ≥ -3 với mọi x.

Vậy trong các tiếp tuyến tại các điểm trên đồ thị hàm số đã cho, tiếp tuyến có hệ số góc nhỏ nhất bằng -3.

Câu 15:

Phương trình tiếp tuyến của đồ thị hàm số y = x⁴ + 2x² – 1 tại điểm có tung độ tiếp điểm bằng 2 là:

A. y = 8x – 6, y = -8x – 6.

B. y = 8x = 6, y = -8x + 6.

C. y = 8x – 8, y = -8x + 8.

D. y = 40x – 57.

Xem đáp án

Chọn A.

Đạo hàm: y’ = 4x³ + 4x.

Tung độ tiếp điểm bằng 2 nên

+Tại M(1; 2), ta có y'(1) = 8 nên phương trình tiếp tuyến là

y = 8( x - 1) + 2 hay y = 8x - 6.

* Tại N(-1; 2), ta có, y'(-1) = - 8 nên phương trình tiếp tuyến là

y= -8( x + 1) + 2 hay y = -8x - 6.

Câu 16:

Cho hàm số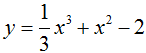 có đồ thị hàm số (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y” = 0 là

Xem đáp án

Chọn A.

Ta có y’ = x² + 2x và y” = 2x + 2

Theo giả thiết x_o là nghiệm của phương trình y”(x_o) = 0

⇔ 2x + 2 = 0 ⇔ x_o = -1

Và y’(-1) = -1

Phương trình tiếp tuyến tại điểm là: y = -1.(x + 1) - 4/3

Hay .

Câu 17:

Cho hàm số 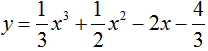.Viết phương trình tiếp tuyến với đồ thị hàm số biết tiếp tuyến song song với đường thẳng d: 4x – y + 2 = 0.

A. y = 4x – 6, y = -4x – 4.

B. y = 4x – 6, y = -4x + 6.

C. y = 2x – 8, y = -2x + 8.

D.Tất cả sai

Xem đáp án

Chọn D.

Gọi M(x_o; y_o) là tiếp điểm của của tiếp tuyến và đồ thị hàm số.

f'(x) = x₀² + x_o – 2.

Viết lại d: y = 4x + 2 ⇒ Hệ số góc k = 4

Vì tiếp tuyến cần tìm song song với d nên:

Với , pttt là:

KL:Có hai tiếp tuyến thỏa mãn ycbt là và .

Câu 18:

Cho hàm số 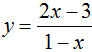.Viết phương trình tiếp tuyến với đồ thị hàm số biết tiếp tuyến vuông góc với đường thẳng d : x – y + 2017 = 0

A. y = - x – 3, y = -x – 1.

B. y = -x – 3, y = -x + 1.

C. y = -x – 8, y = - x + 8.

D.Tất cả sai

Xem đáp án

Chọn B.

Gọi là tiếp điểm của của tiếp tuyến và đồ thị hàm số.

Viết lại d: y = x + 2017 ⇒ Hệ số góc k = 1

Vì tiếp tuyến cần tìm vuông góc với d nên:

Với M(0 ; -3), pttt là: y = -1(x – 0) – 3 ⇒ y = -x – 3.

Với M(-3 ; 1/6), pttt là: y = -(x – 2) – 1 ⇒ y = -x + 1.

Có hai tiếp tuyến thỏa mãn ycbt là y = -x – 3 và y = -x + 1.

Câu 19:

Cho hàm số $y = \frac{3 x - 2}{x - 2}$ .Viết phương trình tiếp tuyến d với đồ thị hàm số biết d tạo với trục hoành một góc α mà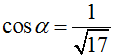

A. y = -4x – 19, y = -4x – 1.

B. y = -4x + 19, y = -x + 3.

C. y = -4x + 19, y = -4x + 3.

D. Tất cả sai

Xem đáp án

Chọn C.

Gọi là tiếp điểm của của tiếp tuyến và đồ thị hàm số.

Trục hoành là đường thẳng có hệ số góc k₁ = 0.

Gọi k₂ là hệ số góc của tiếp tuyến cần tìm. Ta có:

Ta có:

Do đó:

Với M(3; 7), pttt là: y = -4(x – 3) + 7 ⇒ y = -4x + 19.

Với M(1; -1), pttt là: y = -4(x – 1) – 1 ⇒ y = -4x + 3.

Có hai tiếp tuyến thỏa mãn ycbt là y = -4x + 3 và y = -4x + 19.

Câu 20:

Cho hàm số y = x² – 6x + 5 có tiếp tuyến song song với trục hoành. Phương trình tiếp tuyến đó là:

A. x = -3.

B. y = -4.

C. y = 4.

D. x = 3.

Xem đáp án

Chọn B.

Đạo hàm: y’ = 2x – 6.

Trục hoành có phương trình là y = 0

Vì tiếp tuyến song song với trục hoành nên ta có:

y'(x_o) = 0 ⇒ 2x_o – 6 = 0 ⇔ x_o = 3 ⇒ y_o = -4

⇒ Phương trình tiếp tuyến cần tìm là:

y = 0. (x - 3) - 4 hay y = -4.

Câu 21:

Tiếp tuyến của đồ thị hàm số 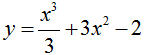có hệ số góc k = -9 có phương trình là:

A. y – 16 = -9(x + 3).

B. y = -9(x + 3).

C. y – 16 = -9(x – 3).

D. y + 16 = -9(x + 3).

Xem đáp án

Chọn A.

Đạo hàm: y’ = x² + 6x.

k = -9 ⇔ y’(x_o) = -9 ⇔ x_o² + 6x_o = -9 ⇔ (x_o + 3)² ⇔ x_o = -3 ⇒ y_o = 16

Phương trình tiếp tuyến cần tìm là (d): y = -9(x + 3) + 16 ⇔ y – 16 = -9(x + 3).

Câu 22:

Cho hàm số 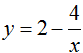có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là

A. y = x + 4.

D. Không tồn tại.

Xem đáp án

Chọn C.

Đạo hàm:

Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 nên có hệ số góc bằng 1.

Ta có phương trình

+ Với x = 2 thì y = 0; y'(2) = 1

Tại M(2; 0). Phương trình tiếp tuyến là y = 1( x – 2)+ 0 = x - 2 .

+ Với x = -2 thì y = 4, y'(-2) = 1

Tại N(-2; 4). Phương trình tiếp tuyến là y = 1.(x + 2) + 4 = x + 6.

Câu 23:

Lập phương trình tiếp tuyến của đường cong (C): y = x³ + 3x² – 8x + 1, biết tiếp tuyến đó song song với đường thẳng Δ: y = x + 2017?

A. y = x + 2018.

B. y = x + 4.

C. y = x – 4; y = x + 28.

D. y = x - 2018.

Xem đáp án

Chọn C.

Đạo hàm: y’ = 3x² + 6x – 8.

Tiếp tuyến cần tìm song song với đường thẳng Δ: y = x + 2017 nên hệ số góc của tiếp tuyến là 1.

Ta có phương trình

+ Với x = 1 thì y(1) = -3 và y'(1) = 1

Tại M(1; -3). Phương trình tiếp tuyến là y =1( x – 1) - 3 =x - 4.

+ Với x = -3 thì y (- 3) = 25 và y'(-3) = 1

Tại N(-3; 25). Phương trình tiếp tuyến là y =1(x + 3) + 25 = x + 28.

Câu 24:

Cho hàm số y = -x³ + 3x² – 2 có đồ thị (C). Số tiếp tuyến của (C) song song với đường thẳng y = -9x là:

A. 1.

B. 3.

C. 4.

D. 2.

Xem đáp án

Chọn D.

Ta có: y’ = -3x² + 6x. Lấy điểm M(x_o; y_o) ∈ (C).

Tiếp tuyến tại Msong song với đường thẳng y = -9x suy ra y’(x_o) = -9

$\Leftrightarrow - 3 x_{0}^{2} + 6 x_{0} = - 9$

Với x_o = -1 ⇒ y_o= 2 ta có phương trình tiếp tuyến: y = - 9( x +1) +2 = -9x - 7

Với x_o = 3 ⇒ y_o= -2 ta có phương trình tiếp tuyến: y = -9( x - 3) - 2 = -9x + 25

Vậy có 2 tiếp tuyến thỏa mãn.

Câu 25:

Cho hàm số y = x³ – 2x² + 2x có đồ thị (C). Gọi x₁, x₂ là hoành độ các điểm M, N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2017. Khi đó x₁ + x₂bằng:

A. 4/3.

B. -4/3.

C. 1/3.

D. -1.

Xem đáp án

Chọn A.

Ta có: y’ = 3x² – 4x + 2.

Tiếp tuyến tại M, N của (C) vuông góc với đường thẳng y = -x + 2017. Nên tiếp tuyến tại M và N có hệ số góc là 1

Hoành độ x₁, x₂ của các điểm M, N là nghiệm của phương trình 3x² – 4x + 2 = 1.

Suy ra x₁ + x₂ = 4/3 ( hệ thức Vi-et).

100 câu trắc nghiệm Đạo hàm cơ bản

100 câu trắc nghiệm Đạo hàm cơ bản (P3)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương