100 câu trắc nghiệm Đạo hàm cơ bản (P1)
-
503 lượt thi
-
25 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Tính đạo hàm của hàm số sau: y = 3x5
 Xem đáp án
Xem đáp án
Chọn B.
Ta có: y = 3x5 nên y’ = (3x5)’ = 3.5x4 = 15x4
Câu 2:
Tính đạo hàm của hàm số sau: y = 2x4 + 2x
 Xem đáp án
Xem đáp án
Chọn C.
Ta có: y = 2x4 + 2x nên y’ = (2x4 + 2x)’ = (2x4)’ + (2x)’ = 8x3 + 2
Câu 3:
Tính đạo hàm của hàm số sau: y = 6x3 – 2x2 + 1
 Xem đáp án
Xem đáp án
Chọn B.
Ta có y = 6x3 – 2x2 + 1 nên y’ = (6x3 )’ – (2x2)’ + 1’ = 18x2 – 4x
Câu 7:
Tính đạo hàm của hàm số sau (a là hằng số)
 Xem đáp án
Xem đáp án
Chọn D.
Ta có:
⇔ y’ = x3 – x2 + x – 1.
Câu 10:
Tính đạo hàm của hàm số sau y = (x2 + 3x)(2 – x).
 Xem đáp án
Xem đáp án
Chọn A.
y’ = ((x2 + 3x)(2 – x))’ = (x2 + 3x)’.(2 – x) + (x2 + 3x).(2 – x)’
= (2x + 3)(2 – x) + (x2 + 3x)(-1)
= -3x2 – 2x + 6.
Câu 11:
Tính đạo hàm của hàm số sau y = (2x – 3)(x5 -2x).
 Xem đáp án
Xem đáp án
Chọn D.
y' = [(2x – 3)(x5 – 2x)]’ = (2x – 3)’(x5 – 2x) + (x5 – 2x)’(2x – 3)
= 2(x5 – 2x) + (5x4 – 2)(2x – 3)
= 12x5 – 15x4 – 8x + 6.
Câu 12:
Tính đạo hàm của hàm số sau y = x(2x - 1)(3x + 2)
 Xem đáp án
Xem đáp án
Chọn B.
Ta có: y = x(2x – 1)(3x + 2) = (2x2 – x)(3x + 2)
y’ = [(2x2 – x)(3x + 2)]’ = (2x2 – x)’(3x + 2) + (3x + 2)’.(2x2 – x)
= (4x – 1)(3x + 2) + 3(2x2 – x)
= 18x2 + 2x – 2.
Câu 13:
Tính đạo hàm của hàm số sau y = (x2 – 2x + 3)(2x2 + 3).
 Xem đáp án
Xem đáp án
Chọn A.
y' = [(x2 – 2x + 3)(2x2 + 3)]’ = (x2 – 2x + 3)’(2x2 + 3) + (2x2 + 3)’ (x2 – 2x + 3)
= (2x – 2)(2x2 + 3) + (4x) (x2 – 2x + 3)
= 8x3 – 12x2 + 18x – 6.
Câu 17:
Cho hàm số f(x) xác định trên R bởi f(x) = 2x2 + 1. Giá trị f’(-1) bằng:
 Xem đáp án
Xem đáp án
Chọn C.
Ta có : f’(x) = 4x ⇒ f’(-1) = -4.
Câu 18:
Cho hàm số f(x) = -x4 + 4x3 – 3x2 + 2x + 1. Giá trị f’(-1) bằng:
 Xem đáp án
Xem đáp án
Chọn D.
Ta có: f’(x) = -4x3 + 12x2 – 6x + 2.
Nên f’(-1) = 24.
Câu 19:
Đạo hàm của hàm số f(x) = (x2 + 1)4 tại điểm x = -1 là:
 Xem đáp án
Xem đáp án
Chọn C.
Ta có : y’ = 4(x2 + 1)3(x2 + 1)’ = 8x(x2 + 1)3
⇒ y’(-1) = -64.
Câu 21:
Cho hàm số f(x) xác định bởi ![]() . Giá trị f’(0) bằng
. Giá trị f’(0) bằng
 Xem đáp án
Xem đáp án
Chọn D.
Ta có :
⇒ f’(x) không xác định tại x = 0
⇒ Hàm số không có đạo hàm tại x = 0.
Câu 25:
Cho f(x) = x5 + x3 – 2x – 3. Tính f’(1) + f’(-1) + 4f(0).
 Xem đáp án
Xem đáp án
Chọn A.
Ta có f’(x) = (x5 + x3 – 2x – 3)’ = 5x4 + 3x2 – 2
f’(1) + f’(-1) + 4f(0) = (5 + 3 – 2) + (5 + 3 – 2) + 4.(-3) = 0

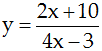
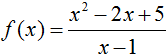
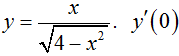 bằng:
bằng: