Giải SGK Toán 7 (Cánh diều) Bài tập cuối chương 4

Giải SGK Bài tập cuối chương 4

Giải Toán 7 trang 108Tập 1

Bài 1 trang 108 Toán lớp 7 Tập 1:

a) Cho một ví dụ về hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh.

b) Thế nào là tia phân giác của một góc?

c) Cho một ví dụ về hai góc đồng vị, hai góc so le trong.

d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị có bằng nhau hay không? Hai góc so le trong có bằng nhau hay không?

e) Phát biểu tiên đề Euclid về đường thẳng song song.

Lời giải:

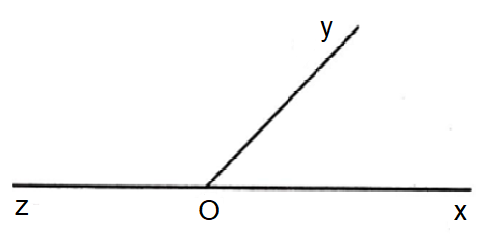
a) Ví dụ: Hai góc xOy và zOy là hai góc kề nhau (như hình vẽ).

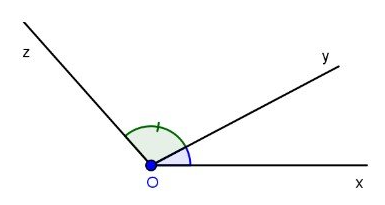
Ví dụ: Hai góc xOy và yOz là hai góc kề bù (như hình vẽ).

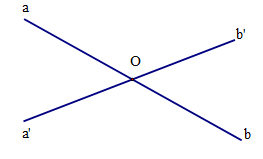
Ví dụ: Hai góc aOb’ và a’Ob là hai góc đối đỉnh.

b) Tia phân giác của một góc là tia nằm trong góc và tạo với hai cạnh của góc đó hai góc bằng nhau.

c) Ví dụ: Hai góc A₃ và B₃ là hai góc đồng vị.

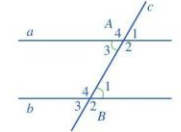
Ví dụ: Hai góc A₃ và B₁ là hai góc so le trong.

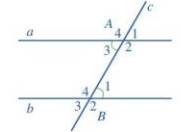
d) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc đồng vị bằng nhau và hai góc so le trong bằng nhau.

e) Tiên đề Euclid về đường thẳng song song:

Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Bài 2 trang 108 Toán lớp 7 Tập 1:

a) Hai góc có tổng số đo bằng 180^o có phải là hai góc kề bù hay không?

b) Hai góc bằng nhau và có chung đỉnh có phải là hai góc đối đỉnh hay không?

Lời giải:

a) Hai góc có tổng số đo bằng 180° không phải là hai góc kề bù.

Vì còn thiếu điều kiện là hai góc đó phải kề nhau.

Hình ảnh minh họa:

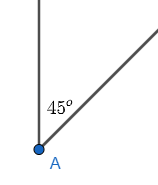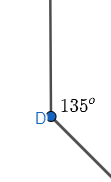 b) Hai góc bằng nhau và có chung đỉnh không phải là hai góc đối đỉnh.

Chẳng hạn: hai góc xOy và x’Oy’ có cung đỉnh O và $\widehat{xOy}=\widehat{x\text{'}Oy\text{'}}$ (như hình vẽ).

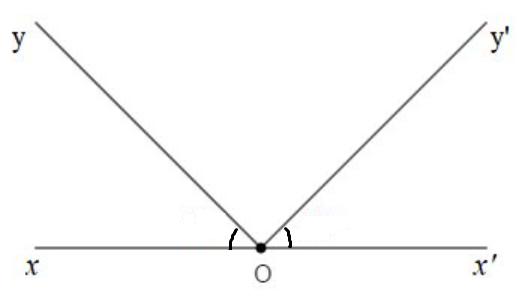
Ta thấy: Hai góc xOy và x’Oy’ không phải là hai góc đối đỉnh, vì tia Ox’ là tia đối của tia Ox nhưng tia Oy’ không phải là tia đối của tia Oy.

Bài 3 trang 108 Toán lớp 7 Tập 1: Tìm cặp đường thẳng song song trong mỗi hình 53a, 53b, 53c, 53d và giải thích vì sao.

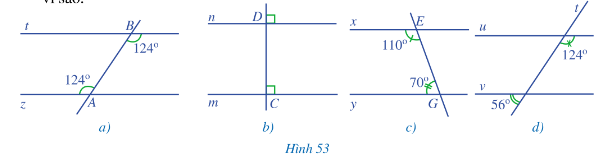
Lời giải:

- Hình 53a:

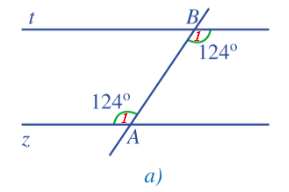
Ta có: ${\widehat{A}}_1$ và ${\widehat{B}}_1$ ở vị trí so le trong và ${\widehat{A}}_1={\widehat{B}}_1={124}^o$.

Do đó t // z.

- Hình 53b:

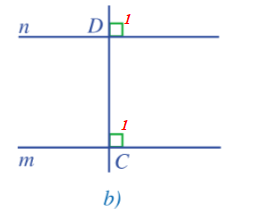
Ta có: ${\widehat{C}}_1$ và ${\widehat{D}}_1$ là hai góc đồng vị và ${\widehat{C}}_1={\widehat{D}}_1={90}^o$

Do đó m // n.

- Hình 53c:

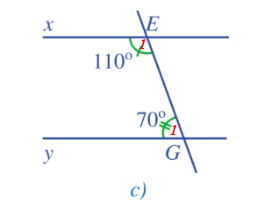
Ta có: ${\widehat{E}}_1$ và ${\widehat{G}}_1$ là hai góc trong cùng phía.

Và ${\widehat{E}}_1={110}^o;{\widehat{G}}_1={70}^o$ nên ${\widehat{E}}_1+{\widehat{G}}_1={110}^o+{70}^o={180}^o$.

Do đó x // y.

- Hình 53d: Gọi giao điểm của hai đường thẳng u và v với đường thẳng t lần lượt tại hai điểm M và N.

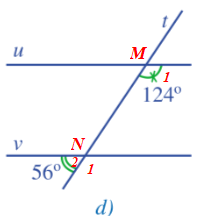
Vì ${\widehat{N}}_1$ và ${\widehat{N}}_2$ là hai góc kề bù nên ${\widehat{N}}_1+{\widehat{N}}_2={180}^o$.

Suy ra ${\widehat{N}}_1={180}^o-{\widehat{N}}_2={180}^o-{56}^o={124}^o$.

Ta có: ${\widehat{M}}_1$ và ${\widehat{N}}_1$ là hai góc đồng vị và ${\widehat{M}}_1={\widehat{N}}_1={124}^o$.

Do đó u // v.

Bài 4 trang 108 Toán lớp 7 Tập 1: Quan sát Hình 54, trong đó Cx song song với AB, đường thẳng BC cắt đường thẳng DE tại F.

a) Tính số đo góc BCx.

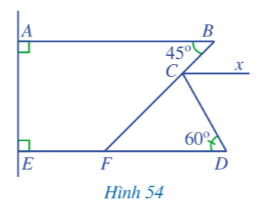
b) Chứng minh rằng Cx song song với DE.

c) Tính số đo góc BCD.

Lời giải:

a) Vì Cx // AB (GT) nên $\widehat{ABC}=\widehat{BCx}=45°$ (hai góc so le trong)

Vậy $\widehat{BCx}=45°.$

b) Vì AB ⊥ AE nên $\widehat{BAE}={90}^o$.

Vì $AE\perp DE$ nên $\widehat{AED}={90}^o$.

Suy ra $\widehat{BAE}+\widehat{AED}={90}^o+{90}^o={180}^o$.

Mà $\widehat{BAE}$ và $\widehat{AED}$ là hai góc trong cùng phía.

Suy ra AB // DE (dấu hiệu nhận biết)

Do đó $\widehat{ABF}=\widehat{BFD}=45°$ (hai góc so le trong)

Suy ra $\widehat{BCx}=\widehat{BFD}=45°$

Mà hai góc $\widehat{BCx}$ và $\widehat{BFD}$ ở vị trí so le trong

Nên Cx // DE (dấu hiệu nhận biết).

b) Theo câu b: Cx // DE nên $\widehat{DCx}=\widehat{CDE}={60}^o$ (hai góc so le trong).

Mà $\widehat{BCx}$và $\widehat{DCx}$ là hai góc kề nhau nên:

$\widehat{BCD}=\widehat{BCx}+\widehat{DCx}={45}^o+{60}^o={105}^o$.

Vậy $\widehat{BCD}={105}^o$.

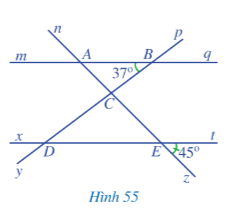
Bài 5 trang 108 Toán lớp 7 Tập 1: Quan sát Hình 55, trong đó mq // xt.

a) Kể tên các cặp góc đồng vị bằng nhau.

b) Tìm số đo các góc BAC, CDE.

c) Bạn Nam cho rằng: Qua điểm C kẻ một đường thẳng song song với hai đường thẳng mq và xt thì sẽ tính được $\widehat{BCE}={82}^o$. Theo em, bạn Nam nói đúng hay sai? Vì sao?

Lời giải:

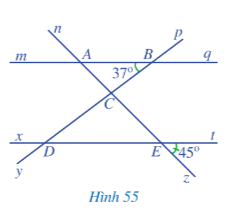
a) Trong Hình 55, các cặp góc đồng vị bằng nhau là:

$\widehat{qAz}=\widehat{tEz}$; $\widehat{mAz}=\widehat{xEz}$;$\widehat{mAn}=\widehat{xEn}$; $\widehat{nAq}=\widehat{nEt}$; $\widehat{mBy}=\widehat{xDy}$; $\widehat{mBp}=\widehat{xDp}$; $\widehat{pBq}=\widehat{pDt};$ $\widehat{qBy}=\widehat{tDy}$.

b) Ta có: $\widehat{CED};\widehat{zEt}$ là hai góc đối đỉnh nên $\widehat{CED}=\widehat{zEt}={45}^o$.

Theo đề bài, mq // xt nên mà hai góc $\widehat{BAC};\widehat{CED}$ ở vị trí so le trong

Nên $\widehat{BAC}=\widehat{CED}$

Do đó $\widehat{BAC}={45}^o$.

Vì mq // xt mà $\widehat{ABC};\widehat{CDE}$ là hai góc so le trong nên $\widehat{ABC}=\widehat{CDE}$.

Mà $\widehat{ABC}=37°$

Do đó $\widehat{CDE}={37}^o$.

Vậy $\widehat{BAC}={45}^o$ và $\widehat{CDE}={37}^o$.

c) Qua điểm C kẻ một đường thẳng c song song với hai đường thẳng mq và xt (như hình vẽ).

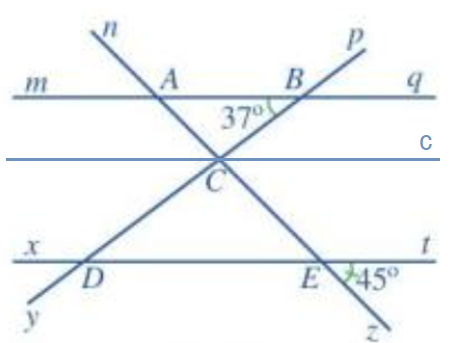
Vì c // mq nên $\widehat{mBC}=\widehat{BCc}$ (hai góc so le trong).

Mà $\widehat{mBC}={37}^o$ nên $\widehat{BCc}={37}^o$.

Vì c // xt nên $\widehat{ECc}=\widehat{CED}$ (hai góc so le trong).

Mà $\widehat{CED}={45}^o$ nên $\widehat{ECc}={45}^o$.

Vì tia Cc nằm giữa hai tia CB và CE nên: $\widehat{BCE}=\widehat{BCc}+\widehat{ECc}$.

Suy ra $\widehat{BCE}={37}^o+{45}^o={82}^o$.

Vậy bạn Nam nói đúng.

Xem thêm lời giải bài tập SGK Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 3

Bài 1: Góc ở vị trí đặc biệt

Bài 2: Tia phân giác của một góc

Bài 3: Hai đường thẳng song song

Bài 4: Định lí