Giải SGK Toán 7 (Kết nối tri thức): Luyện tập chung trang 68

Giải Toán 7 Luyện tập chung trang 68

Giải Toán 7 trang 69 Tập 1

Bài 4.7 trang 69 Toán 7 Tập 1: Các số đo x, y, z trong mỗi tam giác vuông dưới đây bằng bao nhiêu độ?

Lời giải:

+)

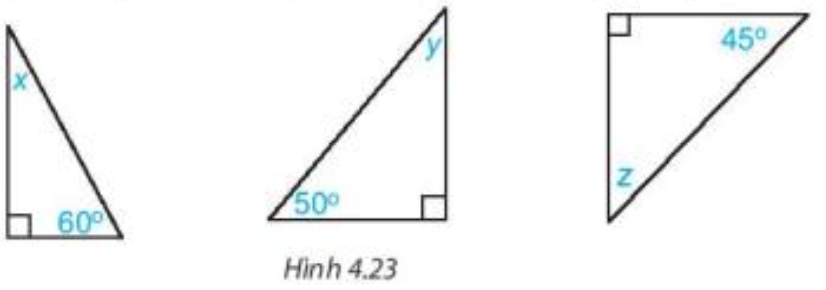
Tam giác trong hình vẽ trên là tam giác vuông nên hai góc nhọn của tam giác phụ nhau.

Do đó x + 60° = 90° suy ra x = 90° – 60° = 30°.

Vậy x = 30°.

+)

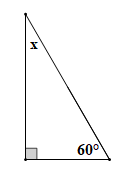
Tam giác trong hình vẽ trên là tam giác vuông nên hai góc nhọn của tam giác phụ nhau.

Do đó y + 50° = 90° suy ra y = 90° – 50° = 40°.

Vậy y = 40°.

+)

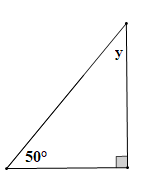
Tam giác trong hình vẽ trên là tam giác vuông nên hai góc nhọn của tam giác phụ nhau.

Do đó z + 45° = 90° suy ra z = 90° – 45° = 45°.

Vậy z = 45°. 

Bài 4.8 trang 69 Toán 7 Tập 1: Tính số đo góc còn lại trong mỗi tam giác dưới đây. Hãy chỉ ra tam giác nào là tam giác vuông.

Lời giải:

+)

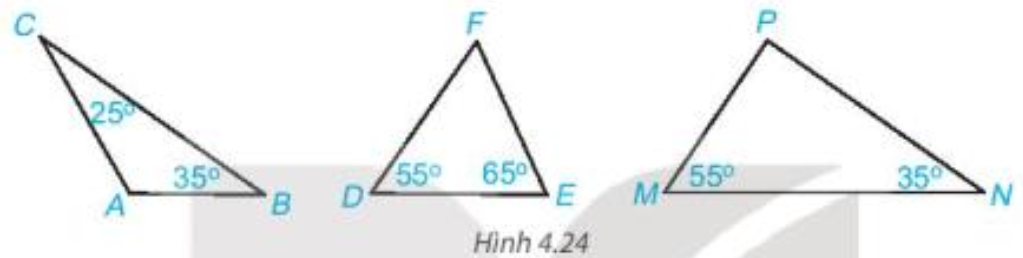
Áp dụng định lí tổng ba góc trong một tam giác cho tam giác ABC (hình vẽ trên) ta có:

$\widehat{A}+\widehat{B}+\widehat{C}=180°$.

Suy ra $\widehat{A}=180°-\widehat{B}-\widehat{C}$

$\widehat{A}=180°-35°-25°$ 

$\widehat{A}=120°$

Vậy $\widehat{A}=120°$

Tam giác ABC có $\widehat{A}=120°$ nên là tam giác tù.

+)

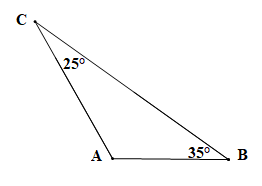
Áp dụng định lí tổng ba góc trong một tam giác cho tam giác DEF (hình vẽ trên) ta có:

$\widehat{D}+\widehat{E}+\widehat{F}=180°$.

Suy ra $\widehat{F}=180°-\widehat{D}-\widehat{E}$

$\widehat{F}=180°-55°-65°$ 

$\widehat{F}=60°$

Vậy $\widehat{F}=60°$

Tam giác DEF có $\widehat{D}=55°,\widehat{E}=65°$ và $\widehat{F}=60°$ đều là góc nhọn nên tam giác DEF là tam giác nhọn.

+)

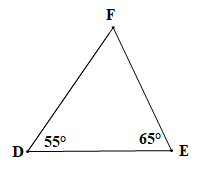
Áp dụng định lí tổng ba góc trong một tam giác cho tam giác MNP (hình vẽ trên) ta có:

$\widehat{M}+\widehat{N}+\widehat{P}=180°$.

Suy ra $\widehat{P}=180°-\widehat{M}-\widehat{N}$

$\widehat{P}=180°-55°-35°$ 

$\widehat{P}=90°$

Vậy $\widehat{P}=90°.$

Tam giác MNP có $\widehat{P}=90°$ là một góc vuông nên là tam giác vuông tại P.

Vậy tam giác MNP là tam giác vuông tại P. 

Bài 4.9 trang 69 Toán 7 Tập 1: Cho Hình 4.25, biết $\widehat{DAC}=60°,$ AB = AC, DB = DC. Hãy tính $\widehat{DAB}.$

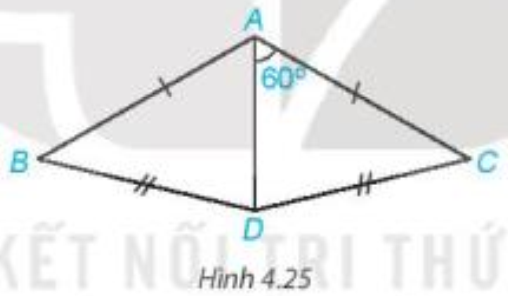
Lời giải:

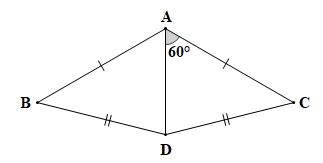
Chứng minh (hình vẽ trên):

Hai tam giác ABD và ACD có:

AB = AC (theo giả thiết);

DB = DC (theo giả thiết);

AD là cạnh chung.

Vậy $\Delta ABD=\Delta ACD$ (c.c.c).

Suy ra $\widehat{DAB}=\widehat{DAC}$ (hai góc tương ứng).

Mà $\widehat{DAC}=60°$(theo giả thiết) do đó $\widehat{DAB}=60°.$

Vậy $\widehat{DAB}=60°.$ 

Bài 4.10 trang 69 Toán 7 Tập 1: Cho tam giác ABC có $\widehat{BCA}=60°$ và điểm M nằm trên cạnh BC sao cho $\widehat{BAM}=20°,\widehat{AMC}=80°$ (H.4.26). Tính số đo các góc AMB, ABC, BAC.

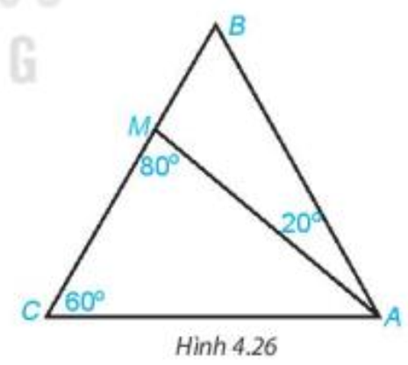
Lời giải:

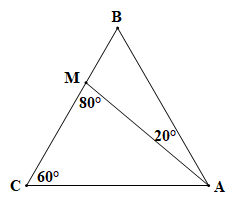
Chứng minh (hình vẽ trên):

+) Điểm M nằm trên cạnh BC nên tia MB là tia đối của tia MC, khi đó góc AMC và góc AMB là hai góc kề bù.

Do đó $\widehat{AMB}+\widehat{AMC}=180°$ (tính chất hai góc kề bù).

Suy ra $\widehat{AMB}=180°-\widehat{AMC}$ 

$\widehat{AMB}=180°-80°=100°$

Vậy $\widehat{AMB}=100°.$ 

+) Xét tam giác AMB có góc AMC là góc ngoài của tam giác tại đỉnh M, do đó $\widehat{AMC}=\widehat{ABM}+\widehat{BAM}$ (tính chất góc ngoài của một tam giác).

Suy ra $\widehat{ABM}=\widehat{AMC}-\widehat{BAM}$

$\widehat{ABM}=80°-20°$

$\widehat{ABM}=60°.$ 

Do đó $\widehat{ABC}=\widehat{ABM}=60°.$ 

Vậy $\widehat{ABC}=60°.$

+) Áp dụng định lí tổng ba góc trong một tam giác cho tam giác ABC với $\widehat{ABC}=60°,$ $\widehat{BCA}=60°$ ta có: $\widehat{BAC}+\widehat{ABC}+\widehat{BCA}=180°$

Suy ra $\widehat{BAC}=180°-\widehat{ABC}-\widehat{BCA}$ 

Hay $\widehat{BAC}=180°-60°-60°$

$\widehat{BAC}=60°.$ 

Vậy $\widehat{BAC}=60°.$ 

Bài 4.11 trang 69 Toán 7 Tập 1: Cho $\Delta ABC=\Delta DEF.$ Biết rằng $\widehat{A}=60°,\widehat{E}=80°,$ tính số đo các góc B, C, D, F.

Lời giải:

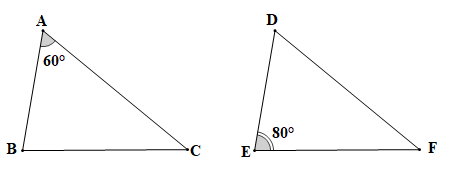
Chứng minh (hình vẽ trên):

Vì $\Delta ABC=\Delta D\text{EF}$ (theo giả thiết) nên $\widehat{A}=\widehat{D},\widehat{B}=\widehat{E},\widehat{C}=\widehat{F}$ (các cặp góc tương ứng).

Mà $\widehat{A}=60°,\widehat{E}=80°$ (theo giả thiết).

Suy ra $\widehat{D}=60°,\widehat{B}=80°.$ 

Áp dụng định lí tổng ba góc trong một tam giác cho tam giác ABC ta có $\widehat{A}+\widehat{B}+\widehat{C}=180°.$

Suy ra $\widehat{C}=180°-\widehat{A}-\widehat{B}$  

Hay $\widehat{C}=180°-60°-80°=40°.$

Mà $\widehat{C}=\widehat{F}$ (chứng minh trên).

Do đó $\widehat{F}=40°.$ 

Vậy $\widehat{B}=80°;\widehat{C}=40;\widehat{D}=60°;\widehat{F}=40°.$ 

Xem thêm lời giải bài tập SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 12: Tổng các góc trong một tam giác

Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Luyện tập chung trang 74

Bài 15: Các trường hợp bằng nhau của tam giác vuông