Giải SGK Toán 11 (Chân trời sáng tạo) Bài 1: Góc lượng giác

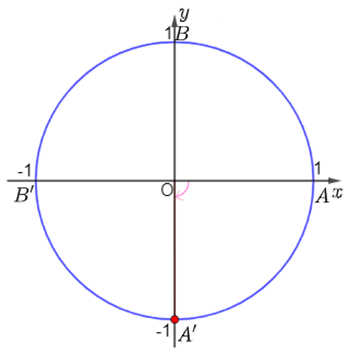
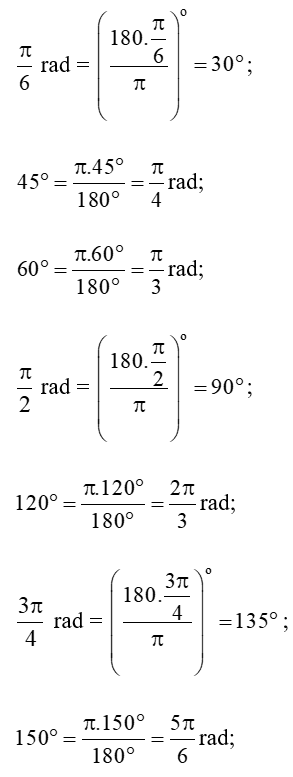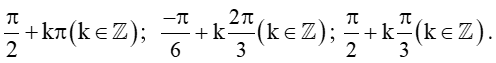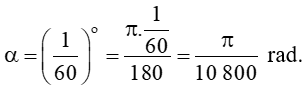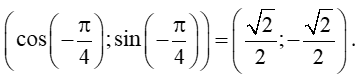Giải Toán 11 Bài 1: Góc lượng giác

Hoạt động khởi động trang 7 Toán 11 Tập 1: Mỗi hình dưới đây thể hiện chuyển động quay của một điểm trên bánh lái tàu từ vị trí A đến vị trí B. Các chuyển động này có điểm nào giống nhau, điểm nào khác nhau?

Lời giải:

Sau bài học này ta sẽ trả lời được như sau:

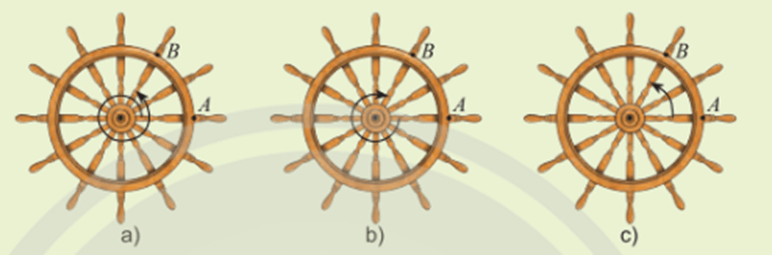
Các chuyển động này có:

+) Điểm chung là: Đều chuyển động quay từ điểm A đến điểm B.

+) Điểm khác là: Góc lượng giác.

1. Góc lượng giác

Khái niệm góc lượng giác

Hoạt động khám phá 1 trang 7 Toán 11 Tập 1: Một chiếc bánh lái tàu có thể quay theo cả hai chiều. Trong Hình 1 và Hình 2, lúc đầu thanh OM ở vị trí OA.

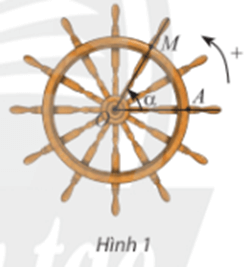
a) Khi quay bánh lái ngược chiều kim đồng hồ (Hình 1), cứ mỗi giây, bánh lái quay một góc 60°. Bảng dưới dây cho ta góc quay α của thanh OM sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hợp.

Thời gian t (giây)	1	2	3	4	5	6
Góc quay α	60°	120°	?	?	?	?

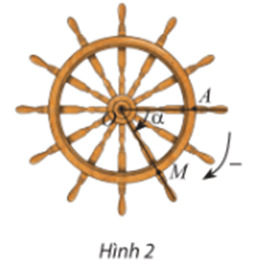
b) Nếu bánh lái được quay theo chiều ngược lại, nghĩa là quay cùng chiều kim đồng hồ (Hình 2) với cùng tốc độ như trên, người ta ghi – 60° để chỉ góc mà thanh OM quay được sau mỗi giây. Bảng dưới đây cho ta góc quay α của thanh OM sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hợp.

Thời gian t (giây)	1	2	3	4	5	6
Góc quay α	– 60°	– 120°	?	?	?	?

Lời giải:

a) Vì cứ mỗi giây, bánh lái quay một góc 60° nên tương ứng ta có:

Với t = 1 (giây) thì α = 60°;

Với t = 2 (giây) thì α = 2.60° = 120°;

Với t = 3 (giây) thì α = 3.60° = 180°;

Với t = 4 (giây) thì α = 4.60° = 240°;

Với t = 5 (giây) thì α = 5.60° = 300°;

Với t = 6 (giây) thì α = 6.60° = 360°;

Khi đó ta có bảng:

Thời gian t (giây)	1	2	3	4	5	6
Góc quay α	60°	120°	180°	240°	300°	360°

b) Vì cứ mỗi giây, bánh lái quay một góc – 60° nên tương ứng ta có:

Với t = 1 (giây) thì α = – 60°;

Với t = 2 (giây) thì α = 2.(– 60°) = – 120°;

Với t = 3 (giây) thì α = 3.(– 60°) = – 180°;

Với t = 4 (giây) thì α = 4.(– 60°) = – 240°;

Với t = 5 (giây) thì α = 5.(– 60°) = – 300°;

Với t = 6 (giây) thì α = 6.(– 60°) = – 360°;

Khi đó ta có bảng:

Thời gian t (giây)	1	2	3	4	5	6
Góc quay α	– 60°	– 120°	– 180°	– 240°	– 300°	– 360°

Thực hành 1 trang 9 Toán 11 Tập 1: Cho $\widehat{MON}=60°$. Xác định số đo của các góc lượng giác được biểu diễn trong Hình 6 và viết công thức tổng quát của số đo góc lượng giác (OM, ON).

Lời giải:

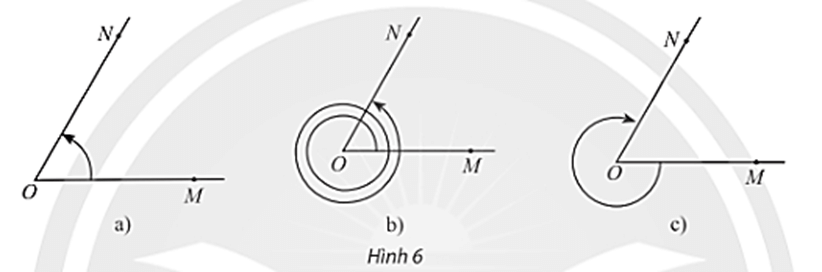
Số đo góc lượng giác (OM, ON) trong Hình 6a là 60°.

Số đo góc lượng giác (OM, ON) trong Hình 6b là 2.360° + 60° = 780°.

Số đo góc lượng giác (OM, ON) trong Hình 6c là – (360° – 60°) = –300°.

Vận dụng 1 trang 9 Toán 11 Tập 1: Trong các khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác bao nhiêu độ?

Lời giải:

Từ 0 giờ đến 2 giờ, kim phút quay được 2 vòng tròn tương ứng với quét một góc: 2.360° = 720°.

Còn 15 phút còn lại kim phút quay quét thêm một góc lượng giác là: 90°.

Vì vậy từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác: 720° + 90° = 810°.

Hệ thức Chasles (Sa-lơ)

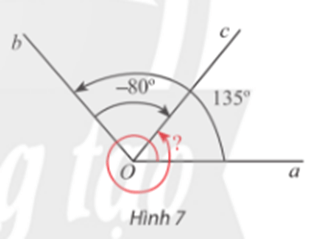
Hoạt động khám phá 2 trang 9 Toán 11 Tập 1: Cho Hình 7:

a) Xác định số đo các góc lượng giác (Oa, Ob), (Ob, Oc) và (Oa, Oc).

b) Nhận xét về mối liên hệ giữa ba số đo góc này.

Lời giải:

a) Số đo của góc lượng giác (Oa, Ob) có tia đầu là Oa và tia cuối là Ob là 135°.

Số đo của góc lượng giác (Ob, Oc) có tia đầu là Ob và tia cuối là Oc là – 80°.

Ta có: $\widehat{aOc}=\widehat{aOb}-\widehat{bOc}=135°-80°=55°$.

Khi đó số đo của góc lượng giác (Oa, Oc) có tia đầu là Oa và tia cuối là Oc là 55° + 360° = 415°.

b) Ta có: 135° + (– 80°) = 415° – 360°.

Vậy (Oa, Ob) + (Ob, Oc) = (Oa, Oc) – 360°.

Vận dụng 2 trang 9 Toán 11 Tập 1: Trong Hình 8, chiếc quạt có ba cánh được phân bố đều nhau. Viết công thức tổng quát số đo của góc lượng giác (Ox, ON) và (Ox, OP).

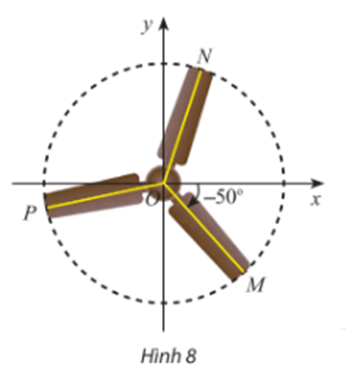
Lời giải:

Chiếc quạt có ba cạnh được phân bố đều nhau nên $\widehat{MON}=\widehat{NOP}=\widehat{POM}=120°$.

+) Với ba tia OM, Ox và ON, ta có:

(Ox, OM) + (OM, ON) = (Ox, ON) + k₁360° (k₁ ∈ ℤ)

⇒ (Ox, ON) = (Ox, OM) + (OM, ON) – k₁360°

⇒ (Ox, ON) = 120° + (– 50°) – k₁360°

⇒ (Ox, ON) = 70° – k₁360°.

+) Với ba tia Ox, ON, OP, ta có:

(Ox, ON) + (ON, OP) = (Ox, OP) + k₂360° (k₂ ∈ ℤ)

⇒ (Ox, OP) = (Ox, ON) + (ON, OP) – k₂360°

⇒ (Ox, OP) = 70° – k₁360° + 120° – k₂360°

⇒ (Ox, OP) = 190° – (k₁ + k₂) 360°

⇒ (Ox, OP) = 190° – k 360° (với k = k₁ + k₂).

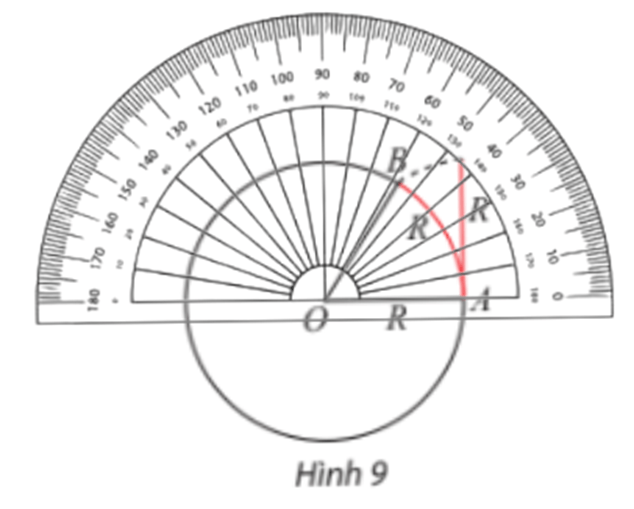
2. Đơn vị radian

Hoạt động khám phá 3 trang 10 Toán 11 Tập 1: Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung  có độ dài đúng bằng R (Hình 9). Đo và cho biết $\widehat{AOB}$ có số đo bằng bao nhiêu độ.

Lời giải:

Tiến hành đo góc $\widehat{AOB}$ ta được $\widehat{AOB}=58°$.

3. Đường tròn lượng giác

Thực hành 2 trang 11 Toán 11 Tập 1: Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:

Số đo theo độ	0°	?	45°	60°	?	120°	?	150°	180°
Số đo theo rad	0 rad	$\frac{\pi }{6}$rad	?	?	$\frac{\pi }{2}$ rad	?	$\frac{3\pi }{4}$ rad	?	$\pi$ rad

Lời giải:

Ta có:

$0°=\frac{\pi .0°}{180°}=0$ rad;

$180°=\frac{\pi .180°}{180°}=\pi$ rad.

Số đo theo độ	0°	30°	45°	60°	90°	120°	135°	150°	180o
Số đo theo rad	0 rad	$\frac{\pi }{6}$ rad	$\frac{\pi }{4}$ rad	$\frac{\pi }{3}$ rad	$\frac{\pi }{2}$ rad	$\frac{2\pi }{3}$ rad	$\frac{3\pi }{4}$rad	$\frac{5\pi }{6}$rad	$\pi$ rad

Hoạt động khám phá 4 trang 11 Toán 11 Tập 1: Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0).

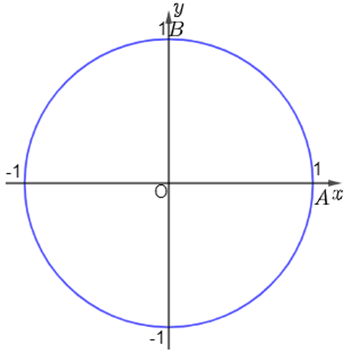
a) Cho điểm B(0; 1). Số đo góc lượng giác (OA, OB) bằng bao nhiêu radian?

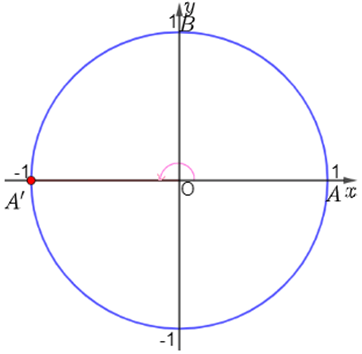
b) Xác định các điểm A’ và B’ trên đường tròn sao cho các góc lượng giác (OA, OA’) và (OA, OB’) có số đo lần lượt là π và $-\frac{\pi }{2}$.

Lời giải:

Ta có hình vẽ:

a) Ta có: Số đo góc lượng giác (OA, OB) bằng 90°.

b) Điểm A’ là điểm nằm trên đường tròn lượng giác thỏa mãn (OA, OA’) bằng π. Khi đó ta có hình vẽ:

Điểm B’ là điểm nằm trên đường tròn lượng giác thỏa mãn (OA, OB’) bằng $-\frac{\pi }{2}$. Khi đó ta có hình vẽ:

Thực hành 3 trang 12 Toán 11 Tập 1: Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo là:

a) – 1 485°;

b) $\frac{19\pi }{4}$.

Lời giải:

a) Ta có: – 1 485° = – 45° + ( – 4).360°.

Biểu diễn góc trên đường tròn lượng giác ta được:

b) Ta có: $\frac{19\pi }{4}=2\pi +\frac{3\pi }{4}$

Biểu diễn góc trên đường tròn lượng giác ta được:

Bài tập

Bài 1 trang 12 Toán 11 Tập 1: Đổi số đo của các góc dưới đây sang radian:

a) 38°;

b) – 115°;

c) ${\left(\frac{3}{\pi }\right)}^o$.

Lời giải:

a) Ta có: 38° = $\frac{\pi .38}{180}=\frac{19\pi }{90}$ rad;

b) – 115° = $\frac{\pi .\left(-115\right)}{180}=-\frac{23\pi }{36}$ rad;

c) ${\left(\frac{3}{\pi }\right)}^o=\frac{\pi .\frac{3}{\pi }}{180}=\frac{1}{60}$ rad.

Bài 2 trang 12 Toán 11 Tập 1: Đổi số đo của các góc sau đây sang độ:

a) $\frac{\pi }{12}$;

b) – 5;

c) $\frac{13\pi }{9}$.

Lời giải:

a) Ta có: $\frac{\pi }{12}$ rad = $\frac{\frac{\pi }{12}.180}{\pi }=15°$.

b) Ta có: – 5 rad = $\frac{5.180}{\pi }={\left(\frac{900}{\pi }\right)}^o$;

c) Ta có: $\frac{13\pi }{9}$ rad = $\frac{\frac{13\pi }{9}.180}{\pi }=26°$.

Bài 3 trang 12 Toán 11 Tập 1: Biểu diễn các góc lượng giác sau trên đường tròn lượng giác:

a) $\frac{-17\pi }{3}$;

b) $\frac{13\pi }{4}$;

c) – 765°.

Lời giải:

a) Ta có: $\frac{-17\pi }{3}=-2.2\pi -\pi -\frac{2\pi }{3}$

Vì vậy điểm biếu diễn góc lượng giác có số đo $\frac{-17\pi }{3}$ là điểm nằm trên phần đường tròn lượng giác thuộc góc phần tư thứ I sao cho $\widehat{A\text{'}OM}=-\frac{2\pi }{3}$ hay $\widehat{A\text{'}OM}=120°$.

Biểu diễn góc này trên đường tròn lượng giác ta được:

b) Ta có: $\frac{13\pi }{4}=2\pi +\pi +\frac{\pi }{4}$

Biểu diễn góc này trên đường tròn lượng giác ta được:

c) Ta có: – 765° = (– 2).360° – 45°

Biểu diễn góc này trên đường tròn lượng giác ta được:

Bài 4 trang 12 Toán 11 Tập 1: Góc lượng giác $\frac{31\pi }{7}$ có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào dưới đây?

$\frac{3\pi }{7};\frac{10\pi }{7};\frac{-25\pi }{7}.$

Lời giải:

Hai góc lượng giác α và β có cùng điểm biểu diễn trên đường tròn lượng giác khi tồn tại số nguyên k khác 0 thỏa mãn: α = k.2π + β

Ta có:

 (thỏa mãn) nên có cùng điểm biểu diễn với góc lượng giác $\frac{3\pi }{7};$

 (không thỏa mãn) nên không có cùng điểm biểu diễn với góc lượng giác $\frac{10\pi }{7};$ (thỏa mãn) nên có cùng điểm biểu diễn với góc lượng giác $\frac{-25\pi }{7}.$

Bài 5 trang 12 Toán 11 Tập 1: Viết các công thức số đo tổng quát của các góc lượng giác (OA, OM) và (OA, ON) trong Hình 14.

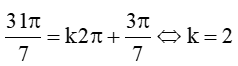
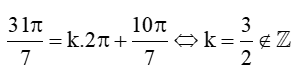
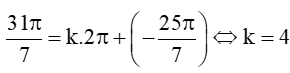
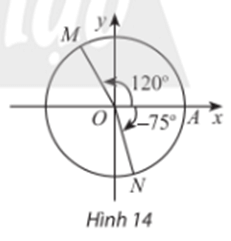
Lời giải:

Công thức số đo tổng quát của các góc lượng giác (OA, OM) là:

(OA, OM) = 120° + k360° (k ∈ ℤ).

Công thức số đo tổng quát của các góc lượng giác (OA, ON) là:

(OA, ON) = – 75° + k360° (k ∈ ℤ).

Bài 6 trang 12 Toán 11 Tập 1: Trong Hình 15, mâm bánh xe ô tô được chia thành năm phần bằng nhau. Viết công thức số đo tổng quát của góc lượng giác (Ox, ON).

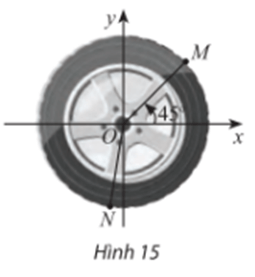
Lời giải:

Vì bánh ô tô được chia làm 5 phần đều nhau nên mỗi phần sẽ có số đo góc là: 360° : 5 = 72°. Góc MON chiếm 2 phần nên có số đo góc là 2.72° = 144°.

Khi đó $\widehat{xON}=\widehat{MON}-\widehat{xOM}=72°-45°=27°$.

Vậy công thức số đo tổng quát của góc lượng giác (Ox, ON) = 27° + k.360°.

Bài 7 trang 13 Toán 11 Tập 1: Trên đường tròn lượng giác hãy biểu diễn các góc lượng giác có số đo có dạng là:

a) $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$;

b) $k\frac{\pi }{4}\left(k\in \mathbb{Z}\right)$.

Lời giải:

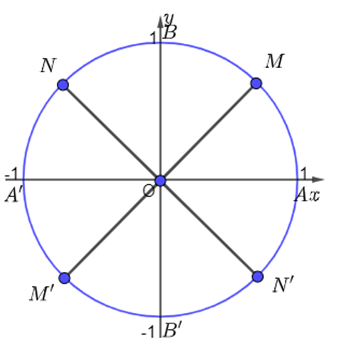
a) Với k = 0 thì có góc lượng giác có số đo góc là $\frac{\pi }{2}$, được biểu diễn bởi điểm M;

Với k = 1 thì có góc lượng giác có số đo góc là $\frac{\pi }{2}+\pi =\frac{3\pi }{2}$, được biểu diễn bởi điểm N;

Với k = 2 thì có góc lượng giác có số đo góc là $\frac{\pi }{2}+2\pi$ nên cũng được biểu diễn bởi điểm M;

Với k = 3 thì có góc lượng giác có số đo góc là $\frac{\pi }{2}+3\pi =\frac{3\pi }{2}+2\pi$ nên cũng được biểu diễn bởi điểm N.

Vậy với k chẵn thì các góc lượng giác có số đo dạng $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bởi điểm M, với k lẻ thì các góc lượng giác có số đo dạng $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bởi điểm N khi đó ta có hình vẽ sau:

b) Với k = 0 thì có góc lượng giác có số đo góc là 0, được biểu diễn bởi điểm A;

Với k = 1 thì có góc lượng giác có số đo góc là $\frac{\pi }{4}$, được biểu diễn bởi điểm M;

Với k = 2 thì có góc lượng giác có số đo góc là $\frac{2\pi }{4}=\frac{\pi }{2}$ được biểu diễn bởi điểm B;

Với k = 3 thì có góc lượng giác có số đo góc là $\frac{3\pi }{4}$ được biểu diễn bởi điểm N;

Với k = 4 thì có góc lượng giác có số đo góc là $\frac{4\pi }{4}=\pi$ được biểu diễn bởi điểm A’;

Với k = 5 thì có góc lượng giác có số đo góc là $\frac{5\pi }{4}$ được biểu diễn bởi điểm M’;

Với k = 6 thì có góc lượng giác có số đo góc là $\frac{6\pi }{4}=\frac{3\pi }{2}$ được biểu diễn bởi điểm B’;

Với k = 7 thì có góc lượng giác có số đo góc là $\frac{7\pi }{4}$ được biểu diễn bởi điểm N’;

Với k = 8 thì có góc lượng giác có số đo góc là $\frac{8\pi }{4}=2\pi +0$ nên được biểu diễn bởi điểm A;

Vậy các góc lượng giác có số đo dạng $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bởi các điểm A, M, B, N, A’, M’, B’, N’. Khi đó ta có hình vẽ sau:

Bài 8 trang 13 Toán 11 Tập 1: Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể biểu diễn cho các góc lượng giác nào sau đây?

Lời giải:

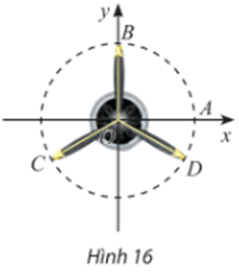
+) Xét các góc lượng giác có số đo $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$

Với k chẵn ta có các góc lượng giác có số đo $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bởi điểm B;

Với k lẻ ta có các góc lượng giác có số đo $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bởi điểm B’(0; – 1).

Vì vậy các điểm B, C, D không thể biểu diễn cho các góc lượng giác có số đo $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$.

+) Xét các góc lượng giác có số đo $\frac{-\pi }{6}+k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right)$

Với k = 0 ta có góc lượng giác có số đo $\frac{-\pi }{6}$ được biểu diễn bởi điểm D.

Với k = 1 ta có góc lượng giác có số đo $\frac{-\pi }{6}+\frac{2\pi }{3}=\frac{\pi }{2}$ được biểu diễn bởi điểm B.

Với k = 2 ta có góc lượng giác có số đo $\frac{-\pi }{6}+2.\frac{2\pi }{3}=\frac{7\pi }{6}$ được biểu diễn bởi điểm C.

Với k = 3 ta có góc lượng giác có số đo $\frac{-\pi }{6}+3.\frac{2\pi }{3}=\frac{-\pi }{6}+2\pi$ được biểu diễn bởi điểm D.

Vì vậy các góc lượng giác có số đo $\frac{-\pi }{6}+k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right)$ được biểu diễn bởi các điểm B, C, D.

+) Xét các góc lượng giác có số đo $\frac{\pi }{2}+k\frac{\pi }{3}\left(k\in \mathbb{Z}\right)$

Với k = 0 ta có góc lượng giác có số đo $\frac{\pi }{2}$ được biểu diễn bởi điểm B.

Với k = 1 ta có góc lượng giác có số đo $\frac{\pi }{2}+\frac{\pi }{3}=\frac{5\pi }{6}$ được biểu diễn bởi điểm M.

Với k = 2 ta có góc lượng giác có số đo $\frac{\pi }{2}+2\frac{\pi }{3}=\frac{7\pi }{6}$ được biểu diễn bởi điểm C.

Với k = 3 ta có góc lượng giác có số đo $\frac{\pi }{2}+3\frac{\pi }{3}=\frac{3\pi }{2}$ được biểu diễn bởi điểm B’.

Với k = 4 ta có góc lượng giác có số đo $\frac{\pi }{2}+4\frac{\pi }{3}=\frac{11\pi }{6}=-\frac{\pi }{6}+2\pi$ được biểu diễn bởi điểm D.

Với k = 5 ta có góc lượng giác có số đo $\frac{\pi }{2}+5\frac{\pi }{3}=\frac{13\pi }{6}=\frac{\pi }{6}+2\pi$ được biểu diễn bởi điểm N.

Với k = 6 ta có góc lượng giác có số đo $\frac{\pi }{2}+6\frac{\pi }{3}=\frac{\pi }{2}+2\pi$ được biểu diễn bởi điểm B.

Ví vậy các điểm B, C, D không thể biểu diễn cho các góc lượng giác có số đo là $\frac{\pi }{2}+k\frac{\pi }{3}\left(k\in \mathbb{Z}\right)$.

Bài 9 trang 13 Toán 11 Tập 1: Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc $\alpha ={\left(\frac{1}{60}\right)}^o$ của đường kinh tuyến (Hình 17). Đổi số đo α sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu ki lô mét, biết bán kính trung bình của Trái Đất là 6 371 km. Làm tròn kết quả hàng phần trăm.

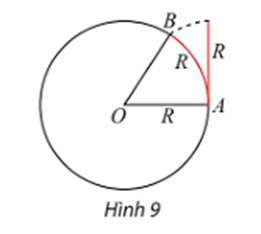
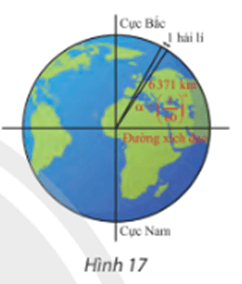
Lời giải:

Ta có: 

Độ dài cung chắn góc α là: α.R = $\frac{\pi }{10800}$.6 371 $\approx$ 1,85 km.

Vậy 1 hải lí bằng 1,85 km.

Hoạt động khởi động trang 13 Toán 11 Tập 1: Hình bên biểu diễn xích đu IA có độ dài 2m dao động quanh trục IO vuông góc với trục Ox trên mặt đất và A’ là hình chiếu của A lên Ox. Tọa độ s của A’ trên trục Ox được gọi là li độ của A và (IO, IA) = α được gọi là li độ góc của A. Làm cách nào để tính li độ dựa vào li độ góc?

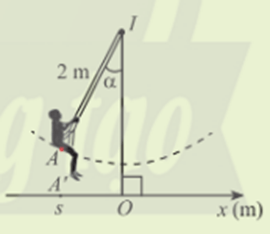
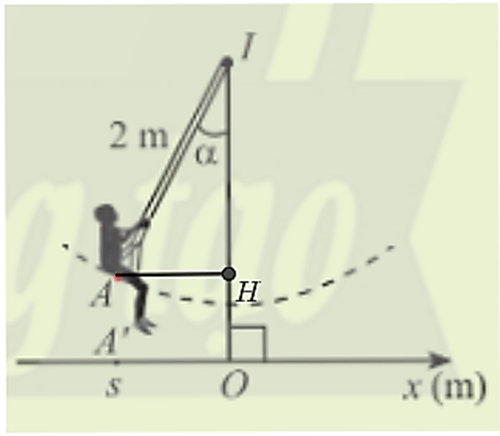
Lời giải:

Kẻ AH vuông góc với IO tại H

Xét tam giác AHI vuông tại H, có:

AH = sinα . IA = 2sinα (m).

AH cũng chính là li độ của A nên s = 2sinα.

Hoạt động khám phá 1 trang 13 Toán 11 Tập 1: Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác $\frac{2\pi }{3}$ và $-\frac{\pi }{4}$ trên đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy.

Lời giải:

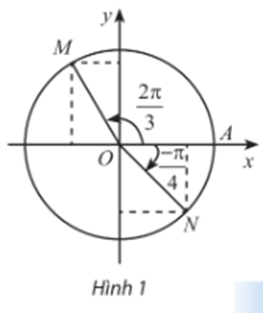
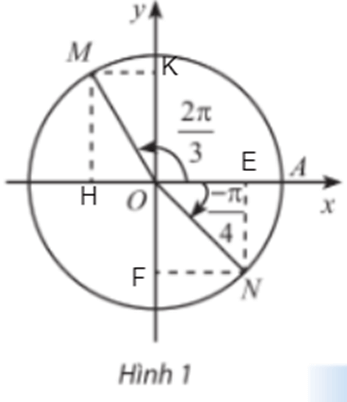
Gọi H, K lần lượt là hình chiếu của điểm M xuống trục Ox và Oy; gọi E, F lần lượt là hình chiếu của điểm N trên trục Ox và Oy.

Đặt (OA, OM) = $\alpha$, (OA, ON) = $\beta$.

+) Xét tam giác MHO vuông tại H, có:

MH = sin$\widehat{MOH}$.MO = sin$\widehat{MOH}$

Ta có $\widehat{MOH}+\widehat{AOM}=180°$ nên sin$\widehat{MOH}$ = sin$\widehat{AOM}$.

⇒ MH = sin$\widehat{AOM}$ = sinα.

Mà MH = OK nên OK = sinα hay tung độ điểm M bằng sinα.

Ta lại có: OH = cos$\widehat{MOH}$.MO = cos$\widehat{MOH}$

Mà $\widehat{MOH}+\widehat{AOM}=180°$ nên cos$\widehat{MOH}$ = -cos$\widehat{AOM}$

⇒ OH = -cos$\widehat{AOM}$ = – cosα do đó hoành độ của điểm M bằng cosα.

Vậy tọa độ điểm M là (cosα; sinα) = $\left(\text{cos}\frac{2\pi }{3};\sin \frac{2\pi }{3}\right)=\left(-\frac{1}{2};\frac{\sqrt{3}}{2}\right)$.

+) Xét tam giác ONE vuông tại E, có:

NE = sin$\widehat{NOE}$.ON = sin$\widehat{NOE}$

Mà $\widehat{NOE}$= -$\beta$

⇒ NE = – sinβ.

Mà NE = OF nên OF = – sinβ do đó tung độ điểm N bằng sinβ.

Ta lại có: OE = cos$\widehat{NOE}$.ON = cos$\widehat{NOE}$

⇒ OE = cosβ nên hoành độ của điểm M bằng cosβ.

Vậy tọa độ điểm N là

(cosβ; sinβ) = 

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 3: Các công thức lượng giác

Bài 4: Hàm số lượng giác và đồ thị giác

Bài 5: Phương trình lượng giác

Bài tập cuối chương 1

 

•