Giải SBT Toán 8 (Cánh diều): Bài tập cuối chương 1

Giải SBT Toán 8 Bài tập cuối chương 1 - Cánh diều

Bài 31 trang 19 SBT Toán 8 Tập 1: Cho hai đa thức: M = 23x²³y ‒ 22xy²³ +21y ‒ 1và N = ‒22xy³ ‒ 42y ‒ 1.

a) Tính giá trị của mỗi đa thức M, N tại x = 0; y = –2.

b) Tính M + N; M – N.

c) Tìm đa thức P sao cho M – N – P = 63y + 1.

Lời giải:

a) Thay x = 0; y = –2 vào M ta có:

M = 23. 0²³.(‒2) ‒ 22.0.².(‒2)²³ +21.(‒2) ‒ 1 = – 42 – 1 = ‒43.

Thay x = 0; y = –2 vào N ta có:

N = ‒22.0.(‒2)³ ‒ 42.(‒2) ‒ 1 = 82 + 1 = 83.

b) Ta có:

M + N = 23x²³y ‒ 22xy²³ + 21y ‒ 1 + (‒ 22xy³ ‒ 42y ‒ 1)

= 23x²³y ‒ 22xy²³ ‒ 22xy³ + (21y – 42y) + (‒1 – 1)

= 23x²³y ‒ 22xy²³ ‒ 22xy³ ‒ 21y ‒ 2.

M + N = 23x²³y ‒ 22xy²³ +21y ‒ 1 – (‒22xy³ ‒ 42y ‒ 1)

= 23x²³y ‒ 22xy²³ +21y ‒ 1 + 22xy³ + 42y + 1

= 23x²³y ‒ 22xy²³ + 22xy³ + 63y.

c) Ta cóM – N – P = 63y + 1

Suy ra P = M – N ‒ (63y + 1)

= 23x²³y ‒ 22xy²³ + 22xy³ + 63y ‒ 63y ‒ 1

= 23x²³y ‒ 22xy²³ + 22xy³ ‒ 1

Bài 32 trang 19 SBT Toán 8 Tập 1: Thực hiện phép tính:

a) $7x^2{y}^5-\frac{7}{3}{y}^2\left(3x^2{y}^3+1\right)$;

b) $\frac{1}{2}x\left(x^2+y^2\right)-\frac{3}{2}{y}^2\left(x+1\right)-\frac{1}{\sqrt{4}}{x}^3$;

c) (x + y)(x² + y² + 3xy) ‒ x³ ‒ y³;

d) (‒132xⁿ⁺¹y¹⁰zⁿ⁺² + 143xⁿ⁺²y¹²zⁿ) : (11xⁿy⁹zⁿ)với n là số tự nhiên.

Lời giải:

a) $7x^2{y}^5-\frac{7}{3}{y}^2\left(3x^2{y}^3+1\right)$

$=7x^2{y}^5-7x^2{y}^5-\frac{7}{3}{y}^2$

$=-\frac{7}{3}{y}^2$.

b) $\frac{1}{2}x\left(x^2+y^2\right)-\frac{3}{2}{y}^2\left(x+1\right)-\frac{1}{\sqrt{4}}{x}^3$

$=\frac{1}{2}{x}^3+\frac{1}{2}x{y}^2-\frac{3}{2}x{y}^2-\frac{3}{2}{y}^2-\frac{1}{2}{x}^3$

$=\left(\frac{1}{2}{x}^3-\frac{1}{2}{x}^3\right)+\left(\frac{1}{2}x{y}^2-\frac{3}{2}x{y}^2\right)-\frac{3}{2}{y}^2$

$=-x{y}^2-\frac{3}{2}{y}^2$.

c) (x + y)(x² + y² + 3xy) ‒ x³ ‒ y³

= (x + y)(x² + y² + 3xy) ‒ (x³ + y³)

= (x + y)(x² + y² + 3xy) ‒ (x + y)(x² ‒ xy + y²)

= (x + y)( x² + y² + 3xy ‒ x² + xy ‒ y²)

= (x + y).4xy

= 4x²y + 4xy².

d) (‒132x^{n + 1}y¹⁰z^{n + 2} + 143x^{n + 2}y¹²zⁿ) : (11xⁿy⁹zⁿ)

= (‒132x^{n + 1}y¹⁰z^{n + 2} : 11xⁿy⁹zⁿ) + (143x^{n + 2}y¹²zⁿ : 11xⁿy⁹zⁿ)

= (‒132 : 11)(x^{n + 1} : xⁿ)(y¹⁰ : y⁹)(z^{n + 2} : zⁿ) + (143 : 11)(x^{n + 2} : xⁿ)(y¹² : y⁹)(zⁿ : zⁿ)

= ‒12xyz² + 13x²y³.

Bài 33* trang 19 SBT Toán 8 Tập 1: Cho a, b, c là ba số tuỳ ý. Chứng minh: Nếu a + b + c = 0 thì a³ + b³ + c³ = 3abc.

Lời giải:

Do a + b + c = 0nên c = ‒a ‒ b.

Khi đó:

a³ + b³ + c³ = a³ + b³ + (‒a ‒ b)³

= a³ + b³ + (‒a)³ ‒ 3(–a)²b + 3(–a)b² ‒ b³

= a³ + b³ ‒ a³ ‒ 3a²b ‒ 3ab² ‒ b³

= ‒3a²b ‒ 3ab² = 3ab(‒a ‒ b) = 3abc

Vậy nếu a + b + c = 0thì a³ + b³ + c³ = 3abc.

Bài 34 trang 19 SBT Toán 8 Tập 1: Tính giá trị của mỗi biểu thức sau:

a) A = 16x² ‒ 8xy + y² ‒ 21biết 4x = y + 1;

b) B = 25x² + 60xy + 36y² + 22biết 6y = 2 ‒ 5x;

c) C = 27x³ – 27x²y + 9xy² – y³ – 121 biết 3x = 7 + y.

Lời giải:

a) A = 16x² ‒ 8xy + y² ‒ 21

= [(4x)² ‒ 2.4x.y + y²] ‒ 21

= (4x ‒ y)² ‒ 21

Mà 4x = y + 1 nên 4x ‒ y = 1

Thay vào A ta có:A = 1² ‒ 21 = ‒20.

b) B = 25x² + 60xy + 36y² + 22

= [(5x)² + 2.5x.6y + (6y)²] +22

= (5x + 6y)² +22

Mà 6y = 2 ‒ 5x nên 5x + 6y = 2

Thay vào B ta có:

B = 2² + 22 = 26.

c) C = 27x³ – 27x²y + 9xy² – y³ – 121

= [(3x)³ ‒ 3.(3x)².y + 3.3x.y² – y³]– 121

= (3x ‒ y)³ ‒ 121

Mà 3x = 7 + ynên 3x ‒ y = 7

Thay vào C ta có:

C = 7³ ‒ 121 = 343 – 121 = 222.

Bài 35 trang 20 SBT Toán 8 Tập 1: Phân tích mỗi đa thức sau thành nhân tử:

a) $3x^2-\sqrt{3}x+\frac{1}{4}$;

b) x² – x – y² + y;

c) x³ + 2x² + x – 16xy².

Lời giải:

a) $3x^2-\sqrt{3}x+\frac{1}{4}={\left(\sqrt{3}x\right)}^2-2.\sqrt{3}x.\frac{1}{2}+{\left(\frac{1}{2}\right)}^2={\left(\sqrt{3}x-\frac{1}{2}\right)}^2$.

b) x² – x – y² + y

= (x² ‒ y²) ‒ (x ‒ y)

= (x ‒ y)(x + y) ‒ (x ‒ y)

= (x ‒ y)(x + y ‒ 1).

c) x³ + 2x² + x – 16xy²

= x(x² + 2x + 1 ‒ 16y²)

= x[(x² + 2x + 1) ‒ 16y²]

= x[(x + 1)² ‒ (4y)²]

= x(x + 1 ‒ 4y)(x + 1 + 4y).

Bài 36 trang 20 SBT Toán 8 Tập 1: Một chiếc khăn trải bàn có dạng hình chữ nhật ABCD được thêu một hoạ tiết có dạng hình thoi MNPQ ở giữa với MP = x (cm), NQ = y (cm) (x > y > 0) như Hình 5.

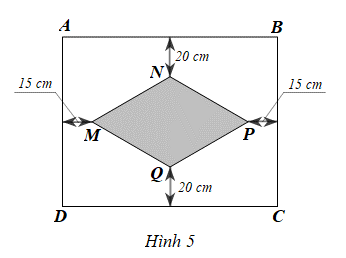
Viết đa thức biểu thị diện tích phần còn lại của chiếc khăn trải bàn đó.

Lời giải:

Diện tích của chiếc khăn trải bàn là:

(15 + x + 15)(20 + y + 20)

= (x + 30)(y + 40) = xy + 40x + 30y + 1200 (cm²)

Diện tích của phần hoạ tiết là: $\frac{1}{2}xy$ (cm²)

Đa thức biểu thị diện tích phần còn lại của chiếc khăn trải bàn đó là:

$xy+40x+30y+1200-\frac{1}{2}xy=\frac{1}{2}xy+40x+30y+1200$(cm²).

Bài 37* trang 20 SBT Toán 8 Tập 1: Tìm số tự nhiên n để n³ – n² + n – 1 là số nguyên tố.

Lời giải:

Ta có:n³ – n² + n – 1

= (n³ ‒ n²) + (n ‒ 1)

= n²(n ‒ 1) + (n ‒ 1)

= (n ‒ 1)(n² + 1).

Với mọi số tự nhiên n, ta có: n ‒ 1 < n² + 1.

Do đó, để n³ – n² + n – 1 là số nguyên tố thì n ‒ 1 = 1 nên .

Khi đó n³ – n² + n – 1 = 5 là số nguyên tố.

Vậy n = 2 thoả mãn yêu cầu của đề bài.

Xem thêm lời giải SBT Toán 8 sách Cánh diều hay, chi tiết khác:

Bài 3: Hằng đẳng thức đáng nhớ

Bài 4: Vận dụng hằng đẳng thức vào phân tích đa thức thành nhân tử

Bài 1: Phân thức đại số

Bài 2: Phép cộng, phép trừ phân thức đại số

Bài 3: Phép nhân, phép chia phân thức đại số