Giải Sách bài tập Toán lớp 7 Bài tập cuối chương 8
Lời giải
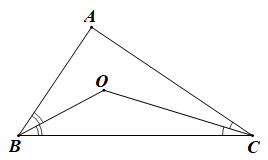
a) Trong ∆CAB ta có: (tổng ba góc trong một tam giác).
Mà (giả thiết).
Suy ra .
Vậy
b) Vì BO là phân giác của góc ABC nên
Vì CO là phân giác của góc ACB nên
Trong COB ta có: (tổng ba góc trong một tam giác).
Mà , , .
Suy ra
Vậy
Lời giải
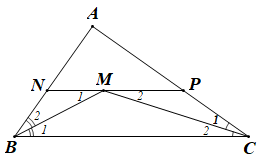
• Ta có: MN // BC (giả thiết) do đó (hai góc so le trong).
Vì BM là phân giác của góc ABC nên .
Suy ra nên tam giác BNM cân tại N.
Do đó BN = NM.
• Ta có: MP // BC (giả thiết) do đó (hai góc so le trong).
Vì CM là phân giác của góc ACB nên .
Suy ra nên tam giác CMP cân tại P.
Do đó PM = PC.
Ta có: NP = MN + MP = BN + CP.
Vậy NP = BN + CP.
Lời giải
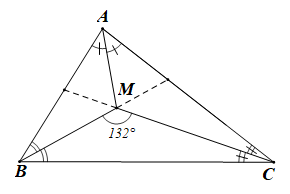
Trong CMB có: (tổng ba góc trong một tam giác).
Suy ra .
Vì BM là phân giác của góc ABC nên .
Vì CM là phân giác của góc ACB nên .
Suy ra .
Trong CAB ta có: (tổng ba góc trong một tam giác).
Suy ra .
Do AM là phân giác góc A của tam giác ABC nên ta có:
.
Vậy
b) Hãy so sánh các đoạn AM và AN.
Lời giải
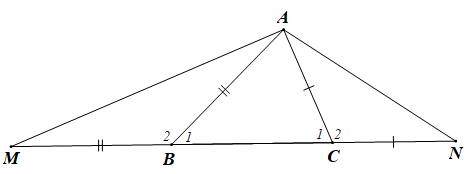
a) Xét ABC có AB > AC (giả thiết) nên (trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn) (1)
Vì CN = CA (giả thiết) nên tam giác ANC cân tại C.
Suy ra (tính chất tam giác cân).
Mặt khác (tổng ba góc trong tam giác CAN).
Do đó
Mà (hai góc kề bù) nên
Suy ra (2)
Tương tự với tam giác BAM ta có: (3).
Từ (1), (2), (3) suy ra .
Vậy .
b) Xét tam giác ANM có (do )
Do đó AM > AN (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn).
Vậy AM > AN.
Lời giải
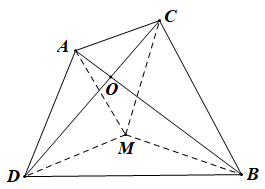
Xét ABM có: MA + MB ≥ AB (bất đẳng thức trong tam giác)
Xét CDM có: MC + MD ≥ CD (bất đẳng thức trong tam giác)
Suy ra MA + MB + MC + MD ≥ AB + CD.
Nên MA + MB + MC + MD nhỏ nhất khi và chỉ khi:
MA + MB + MC + MD = AB + CD
Khi đó MA + MB = AB và MC + MD = CD
Điều này chỉ xảy ra khi M trùng với điểm O.
Vậy khi điểm M là giao điểm của AB và CD thì MA + MB + MC + MD nhỏ nhất.
Bài 6 trang 65 SBT Toán 7 Tập 2:
Lời giải
a) Cho tam giác ABC. Vẽ đường cao AH và đường trung tuyến AM.
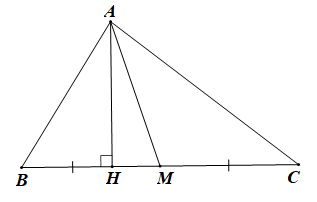
Ta có AH là đường vuông góc, AM là đường xiên.
Suy ra AH ≤ AM (mối quan hệ giữa đường vuông góc và đường xiên).
Vậy trong một tam giác, đường cao không lớn hơn đường trung tuyến xuất phát từ cùng một đỉnh.
b) Cho tam giác ABC. Vẽ đường cao AH và đường phân giác AD.
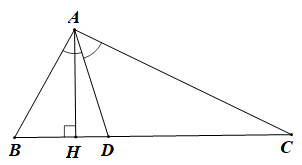
Ta có AH là đường vuông góc, AD là đường xiên.
Suy ra AH ≤ AD (mối quan hệ giữa đường vuông góc và đường xiên).
Vậy trong một tam giác, đường cao không lớn hơn đường phân giác xuất phát từ cùng một đỉnh.
Lời giải
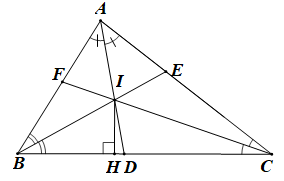
Vì BI là phân giác của góc ABC nên .
Vì CI là phân giác của góc ACB nên .
Vì AI là phân giác của góc ACB nên .
Ta có: (hai góc kề bù).
Do đó (1)
Trong AIC có (tổng ba góc trong một tam giác).
Suy ra (2)
Từ (1) và (2) ta có:
Nên .
Trong CAB ta có: (tổng ba góc trong một tam giác)
Nên
Suy ra (3)
Vì tam giác BIH vuông tại H nên .
Suy ra (4)
Từ (3) và (4) suy ra .
Vậy .
Bài 8 trang 66 SBT Toán 7 Tập 2:
Lời giải
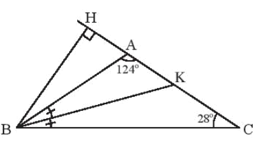
Vì tam giác ABC cân tại A (giả thiết)
Nên (tính chất tam giác cân)
Trong DCAB ta có: (tổng ba góc trong một tam giác).
Mà (giả thiết), (chứng minh trên).
Suy ra .
Vì BK là phân giác của góc ABC nên .
Trong KAB ta có: (tổng ba góc trong một tam giác).
Suy ra .
Vì tam giác BKH vuông tại H nên và .
Suy ra .
Vậy tam giác BHK có
Lời giải
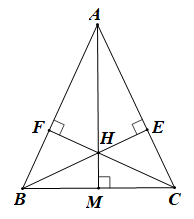
Tam giác ABC có hai đường cao BE và CF cắt nhau tại H nên H là trực tâm của tam giác.
Do đó AH là đường cao ứng với cạnh BC.
Kéo dài AH cắt BC tại M.
Khi đó AH ⊥ BC tại M (1)
Vì tam giác ABC cân tại A (giả thiết) nên AB = AC.
Xét ΔBMA và ΔCMA có:
,
AM là cạnh chung,
AB = AC (chứng minh trên)
Do đó ΔBMA = ΔCMA (cạnh huyền – cạnh góc vuông).
Suy ra BM = CM (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra AH ⊥ BC tại trung điểm M của BC.
Do đó AH là đường trung trực của BC.
Vậy AH là đường trung trực của BC.
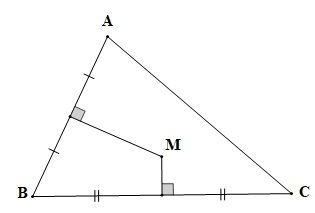
a) Điểm M cách đều ba đỉnh của tam giác ABC.
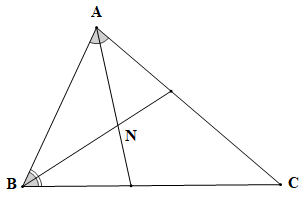
b) Điểm N cách đều ba cạnh của tam giác ABC.
c) Điểm P là trọng tâm của tam giác ABC.
d) Điểm Q là trực tâm của tam giác ABC.
Lời giải
a) Điểm M cách đều ba đỉnh của tam giác ABC nên điểm M là giao điểm của ba đường trung trực của tam giác ABC.
Do ba đường trung trực của một tam giác luôn đi qua một điểm, nên giao điểm của hai trong ba đường trung trực cũng thuộc đường trung trực còn lại.
Ta vẽ hai đường trung trực của AB và BC, giao điểm của hai đường trung trực đó là điểm M (hình vẽ).
b) Điểm N cách đều ba cạnh của tam giác ABC nên điểm N là giao điểm của ba đường phân giác trong của tam giác ABC.
Do ba đường phân giác của một tam giác luôn đi qua một điểm, nên giao điểm của hai trong ba đường phân giác cũng thuộc đường phân giác còn lại.
Ta vẽ hai đường phân giác của góc A và góc B, giao điểm của hai đường phân giác này là điểm N (hình vẽ).
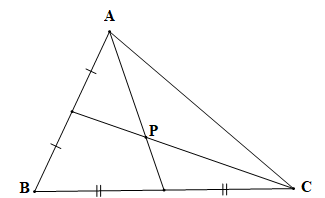
c) Điểm P là trọng tâm của tam giác ABC nên điểm P là giao điểm của ba đường trung tuyến của tam giác ABC.
Do ba đường trung tuyến của một tam giác luôn đi qua một điểm, nên giao điểm của hai trong ba đường trung tuyến cũng thuộc đường trung tuyến còn lại.
Ta vẽ hai đường trung tuyến xuất phát từ đỉnh A và C của tam giác, giao điểm của hai đường trung tuyến này là điểm P (hình vẽ).
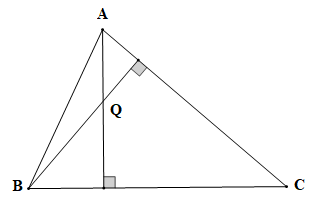
d) Điểm Q là trực tâm của tam giác ABC nên điểm Q là giao điểm của ba đường cao của tam giác ABC.
Do ba đường cao của một tam giác luôn đi qua một điểm, nên giao điểm của hai trong ba đường cao cũng thuộc đường cao còn lại.
Ta vẽ hai đường cao xuất phát từ đỉnh A và đỉnh B của tam giác, giao điểm của hai đường cao này là trực tâm Q của tam giác (hình vẽ).
Xem thêm lời giải sách bài tập Toán lớp 7 bộ sách Chân trời sáng tạo hay, chi tiết nhất:
Bài 8: Tính chất ba đường cao của tam giác
Bài 9: Tính chất ba đường phân giác của tam giác
Bài 1: Làm quen với yếu tố ngẫu
Bài 2: Làm quen với xác xuất của biến cố ngẫu nhiên




