Bài 9 trang 66 SBT Toán 7 Tập 2: Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Chứng minh AH là đường trung trực của BC.
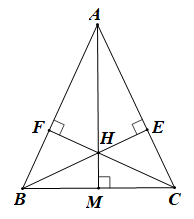
Tam giác ABC có hai đường cao BE và CF cắt nhau tại H nên H là trực tâm của tam giác.
Do đó AH là đường cao ứng với cạnh BC.
Kéo dài AH cắt BC tại M.
Khi đó AH ⊥ BC tại M (1)
Vì tam giác ABC cân tại A (giả thiết) nên AB = AC.
Xét ΔBMA và ΔCMA có:
,
AM là cạnh chung,
AB = AC (chứng minh trên)
Do đó ΔBMA = ΔCMA (cạnh huyền – cạnh góc vuông).
Suy ra BM = CM (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra AH ⊥ BC tại trung điểm M của BC.
Do đó AH là đường trung trực của BC.
Vậy AH là đường trung trực của BC.
Xem thêm lời giải sách bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 8: Tính chất ba đường cao của tam giác
Bài 9: Tính chất ba đường phân giác của tam giác
Bài 1: Làm quen với yếu tố ngẫu