Cho tam giác ABC cân tại A và cho  Vẽ đường cao BH và phân giác BK ứng với đỉnh B của tam giác ABC

Bài 8 trang 66 SBT Toán 7 Tập 2:

Cho tam giác ABC cân tại A và cho $\widehat{A}=124°.$ Vẽ đường cao BH và phân giác BK ứng với đỉnh B của tam giác ABC. Tính số đo các góc của tam giác BHK.

Trả lời

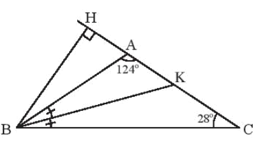
Vì tam giác ABC cân tại A (giả thiết)

Nên $\widehat{ABC}=\widehat{ACB}$ (tính chất tam giác cân)

Trong DCAB ta có: $\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$ (tổng ba góc trong một tam giác).

Mà $\widehat{BAC}=124°$(giả thiết), $\widehat{ABC}=\widehat{ACB}$ (chứng minh trên).

Suy ra $\widehat{ABC}=\widehat{ACB}=\frac{180°-\widehat{BAC}}{2}$$=\frac{180°-124°}{2}=28°$.

Vì BK là phân giác của góc ABC nên $\widehat{ABK}=\widehat{KBC}=\frac{\widehat{ABC}}{2}=\frac{28°}{2}=14°$.

Trong $∆$KAB ta có: $\widehat{ABK}+\widehat{KAB}+\widehat{AKB}=180°$ (tổng ba góc trong một tam giác).

Suy ra $\widehat{AKB}=180°-\widehat{ABK}-\widehat{KAB}$$=180°-14°-124°=42°$.

Vì tam giác BKH vuông tại H nên $\widehat{KHB}=90°$ và $\widehat{HKB}+\widehat{HBK}=90°$.

Suy ra $\widehat{HBK}=90°-\widehat{HKB}=90°-42°=48°$.

Vậy tam giác BHK có $\widehat{HBK}=48°,\widehat{BKH}=42°,\widehat{KHB}=90°.$

Xem thêm lời giải sách bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 8: Tính chất ba đường cao của tam giác

Bài 9: Tính chất ba đường phân giác của tam giác

Bài tập cuối chương 8

Bài 1: Làm quen với yếu tố ngẫu 

Bài 2: Làm quen với xác xuất của biến cố ngẫu nhiên

Bài tập cuối chương 9