Giải Sách bài tập Toán lớp 7 Bài tập cuối chương 2
Giải SBT Toán 7 trang 64 Tập 1
Bài 72 trang 64 SBT Toán 7 Tập 1: Phát biểu nào sau đây là sai?
A. Mọi số vô tỉ đều là số thực.
B. Mọi số thực đều là số vô tỉ.
C. Số 0 là số hữu tỉ.
D. -√2 là số vô tỉ.
Lời giải:
Số thực bao gồm số hữu tỉ và số vô tỉ nên phát biểu "Mọi số thực đều là số vô tỉ" là sai.
Ví dụ: 12 là số thực nhưng không phải là số vô tỉ.
Chọn đáp B.
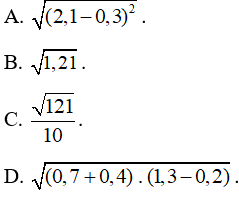
Lời giải:
Tính kết quả ở mỗi đáp án, ta được:
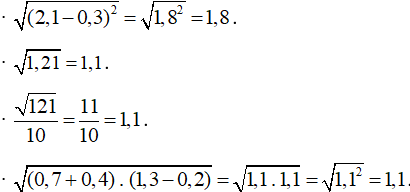
Ta thấy chỉ có phép tính √(2,1−0,3)2 có kết quả không bằng 1,1.
Chọn đáp án A.
Bài 74 trang 64 SBT Toán 7 Tập 1: Tổng các giá trị của x thỏa mãn |x−12|−1=52 là:
A. 4.
B. −3.
C. 1.
D. −1.
Lời giải:
Bài 75 trang 64 SBT Toán 7 Tập 1:
Sắp xếp các số |−4|; √5; |−113|; √64; −73 theo thứ tự tăng dần là:
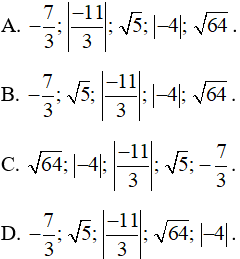
Lời giải:
Ta thấy -73 là số âm; các số còn lại đều là số dương.
Ta có:
|−4|=4; √5=2,236...; |−113|=113=3,(6); √64=8
Vì 2,236... < 3,(6) < 4 < 8 nên √5<|−113|<|−4|<√64.
Do đó −73<√5<|−113|<|−4|<√64.
Vậy các số được sắp xếp theo thứ tự tăng dần là −73; √5; |−113|; |−4|; √64.
Chọn đáp án B.
A. Lớp 7A ủng hộ 3 600 000 đồng; Lớp 7B ủng hộ 4 800 000 đồng.
B. Lớp 7A ủng hộ 4 600 000 đồng; Lớp 7B ủng hộ 3 800 000 đồng.
C. Lớp 7A ủng hộ 3 800 000 đồng; Lớp 7B ủng hộ 4 600 000 đồng.
D. Lớp 7A ủng hộ 4 800 000 đồng; Lớp 7B ủng hộ 3 600 000 đồng.
Lời giải:
Gọi x (đồng), y (đồng) lần lượt là số tiền lớp 7A, 7B ủng hộ cho quỹ phòng chống dịch Covid-19.
Theo đề bài, hai lớp 7A, 7B đã ủng hộ 8 400 000 đồng nên
x + y = 8 400 000.
Số tiền ủng hộ của hai lớp 7A, 7B lần lượt tỉ lệ với 4; 3 nên:
x4=y3=x+y4+3=8 400 0007=1 200 000.
Do đó x = 1 200 000 . 4 = 4 800 000 (đồng);
y = 1 200 000 . 3 = 3 600 000 (đồng).
Vậy số tiền lớp 7A, 7B ủng hộ cho quỹ phòng chống dịch Covid-19 lần lượt là 4 800 000 đồng và 3 600 000 đồng.
Chọn đáp án D.
A. v và t là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ 135.
B. v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 1135.
C. v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 135.
D. v và t là hai đại lượng tỉ lệ thuận với hệ số tỉ lệ 1135.
Lời giải:
Theo đề bài, quãng đường ô tô đi được là 135 km nên v . t = 135.
Do đó v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ v . t = 135.
Chọn đáp án C.
Giải SBT Toán 7 trang 65 Tập 1
13; 176; 34; −1411; −455.
Lời giải:
Các số viết được dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn như sau:
13=1:3=0,(3); 176=17:6=2,8(3); 34=3:4=0,75
−1411=−14:11=−1,(27); −455=−4:55=−0,0(72)
Bài 79 trang 65 SBT Toán 7 Tập 1: Trong các số sau, số nào là số vô tỉ:
34,(3); 5,234561213141516...; −45,8(89); −√121; √19; √2516?
Lời giải:
Ta có: −√121=−11; √19=4,35889...; √2516=54.
Các số 34,(3); −45,8(89); −11; 54 là số hữu tỉ.
Các số 5,234561213141516...; 4,35889... là số vô tỉ.
Vậy các số vô tỉ là 5,234561213141516...; √19.
Bài 80 trang 65 SBT Toán 7 Tập 1: So sánh:
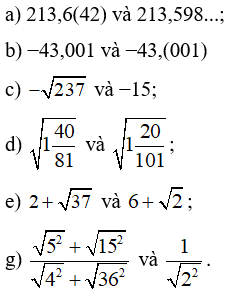
Lời giải:
a) Phần nguyên của hai số 213,6(42) và 213,598... bằng nhau.
Ta so sánh chữ số hàng phần mười, vì 6 > 5 nên 213,6(42) > 213,598...
Vậy 213,6(42) > 213,598...
b) Ta có: −43,(001) = −43,001001...
Vì −43,001 > −43,001001... nên −43,001 > −43,(001).
Vậy −43,001 > −43,(001).
c) Ta có: −√237=−15,3948...
Vì −15,3948... < −15 nên −√237 < −15.
Vậy −√237 < −15.
d) Ta thấy 4081<40202=20101 nên 14081<120101.
Mà 14081>1; 120101>1.
Do đó √14081 > √120101.
e) Ta có: 2+√37=8,0827...; 6+√2=7,4142...
Ta thấy 8,0827... > 7,4142...
Do đó 2+√37 > 6+√2.
g) Ta có: √52+√152√42+√362=5+154+36=2040=12; 1√22=12.
Ta thấy √52+√152√42+√362=12=1√2.
Vậy √52+√152√42+√362=1√2.
Bài 81 trang 65 SBT Toán 7 Tập 1: Sắp xếp các số sau theo thứ tự tăng dần:
a) −0,34; −6,(25); 159; √169; √15;
b) 1,0(09); √64; 3115; 34,(5); −√225.
Lời giải:
a) Ta có −6,(25)=−6,2525...; 159=1,5555...;
√169=13; √15=3,8729....
Vì −6,2525... < −0,34 < 1,5555... < 3,8729... < 13.
Nên −6,(25)<−0,34<159<√15<√169.
Vậy các số được sắp xếp theo thứ tự tăng dần là 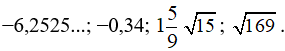
b) Ta có 1,0(09)=1,00909...; √64=8;
3115=31,2; 34,(5)=34,555...; −√225=−15
Vì −15 < 1,00909... < 8 < 31,2 < 34,555...
Nên −√225<1,0(09)<√64<3115<34,(5).
Vậy các số được sắp xếp theo thứ tự tăng dần là −√225; 1,0(09); √64; 3115; 34,(5).
Bài 82 trang 65 SBT Toán 7 Tập 1: Sắp xếp các số sau theo thứ tự giảm dần:
a) 214; √16; −√83; −√196; −0,0(51);
b) 2116; √49; −√144; .
Lời giải:
a) Ta có
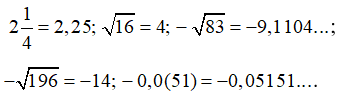
Vì 4 > 2,25 > −0,05151... > −9,1104... > −14.
Nên .
Vậy các số được sắp xếp theo thứ tự giảm dần:;; .
b) Ta có:
−111,0(3) = −111,0333...
Vì 21,166... > 7 > −12 > −111,0333... > −614,1.
Nên .
Vậy các số được sắp xếp theo thứ tự giảm dần:.
Bài 83 trang 65 SBT Toán 7 Tập 1: Tính:
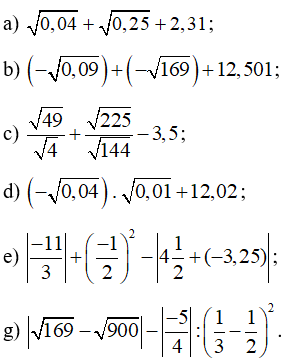
Lời giải:
a)
= 0,2 + 0,5 + 2,31
= 0,7 + 2,31 = 3,01.
b)
= (− 0,3) + (−13) + 12,501
= (−13,3) + 12,501 = −0,799.
c)
= 3,5 + 1,25 – 3,5
= 3,5 – 3,5 + 1,25
= 1,25.
d)
= (–0,2) . 0,1 + 12,02
= –0,02 + 12,02 = 12.
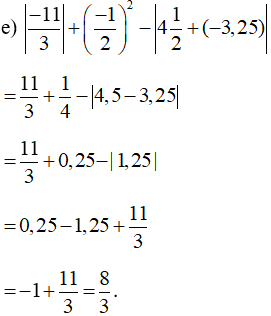
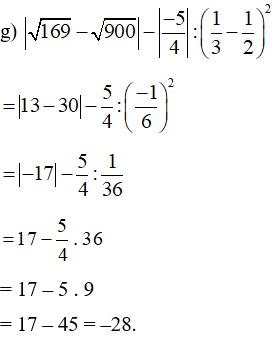
Giải SBT Toán 7 trang 66 Tập 1
Bài 84 trang 66 SBT Toán 7 Tập 1: Tìm x, biết:
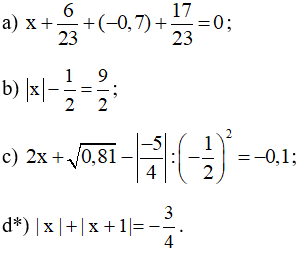
Lời giải:
a)
1 – 0,7 + x = 0
0,3 + x = 0
x = –0,3.
Vậy x = –0,3.
b)
|x| = 5
x = 5 hoặc x = −5.
Vậy x = 5 hoặc x = −5.
c)
0,9 – 5 + 2x = −0,1
– 4,1 + 2x = −0,1
– 4 + 2x = 0
2x = 4
x = 2
Vậy x = 2.
d*) Ta có: |x| ≥ 0; |x + 1| ≥ 0 với mọi số thực x.
Nên |x| + |x + 1| ≥ 0 với mọi số thực x.
Mà nên không có giá trị nào của x thỏa mãn yêu cầu của đề bài.
|
Thời điểm |
Cuối tháng 6 |
Cuối tháng 7 |
Cuối tháng 8 |
Cuối tháng 9 |
|
Chỉ số đồng hồ đo nước (m3) |
204 |
220 |
237 |
250 |
Tổng số tiền nước nhà bạn Hạnh phải trả trong Quý III là 354 200 đồng. Tính số tiền nước nhà bạn Hạnh phải trả trong mỗi tháng của Quý III, biết rằng giá mỗi mét khối nước hằng tháng là như nhau.
Lời giải:
Số nước nhà bạn Hạnh dùng trong Quý III là:
250 – 204 = 46 (m3).
Giá của 1 m3 nước là:
354 200 : 46 = 7 700 (đồng).
Số tiền nước nhà bạn Hạnh phải trả trong tháng 7 là:
7 700 . (220 – 204) = 123 200 (đồng).
Số tiền nước nhà bạn Hạnh phải trả trong tháng 8 là:
7 700 . (237 – 220) = 130 900 (đồng).
Số tiền nước nhà bạn Hạnh phải trả trong tháng 9 là:
7 700 . (250 – 237) = 100 100 (đồng).
Vậy trong Quý III, số tiền nước nhà bạn Hạnh phải trả trong tháng 7, tháng 8, tháng 9 lần lượt là: 123 200 đồng; 130 900 đồng; 130 900 đồng.
Bài 86 trang 66 SBT Toán 7 Tập 1: Tìm ba số x, y, z, biết:
a) 2x = 3y; 5y = 7z và 3x – 7y + 5z = 30;
b) và x – 2y + 3z = 14.
Lời giải:
a) Ta có 2x = 3y; 5y = 7z hay .
Suy ra: .
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
.
Do đó x = 2 . 21 = 42; y = 2 . 14 = 28; z = 2 . 10 = 20.
Vậy x = 42; y = 28; z = 20.
b) và x – 2y + 3z = 14.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
.
Do đó x – 1 = 1 . 2 = 2; y – 2 = 1 . 3 = 3; z – 3 = 1 . 4 = 4.
Vậy x = 3; y = 5; z = 7.
Lời giải:
Ta có quãng đường CB bằng 0,6 lần quãng đường AB nên quãng đường AC bằng 0,4 lần quãng đường AB.
Gọi vận tốc của xe đạp, xe máy lần lượt là v1 (km/h), v2 (km/h).
Do cùng một thời gian thì vận tốc và quãng đường là hai đại lượng tỉ lệ thuận nên
hay .
Mặt khác, ta lại có v2 – v1 = 18.
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
.
Do đó v1 = 6 . 2 = 12 (km/h); v2 = 6 . 5 = 30 (km/h).
Vậy vận tốc của xe đạp, xe máy lần lượt là: 12 km/h; 30 km/h.
Lời giải:
Gọi x (đồng) là giá tiền của một ki-lô-gam trước khi giảm giá.
Giá tiền một ki-lô-gam sau khi giảm giá là:
(100% − 20%) . x = 80%x = 0,8x (đồng).
Số tiền ban đầu chị Hà có: 15x (đồng).
Với số tiền đã chuẩn bị, chị Hà mua được nhiều nhất số kg cá hồi là:
15x : 0,8x = 18,75 (kg)
Ban đầu chị Hà dự định mua 15 kg, sau khi giảm giá thì với số tiền đã chuẩn bị, chị Hà mua thêm được nhiều nhất số kg cá hồi là:
18,75 – 15 = 3,75 (kg) .
Vậy với số tiền đã chuẩn bị, chị Hà mua thêm được nhiều nhất 3,75 ki-lô-gam cá hồi.
Giải SBT Toán 7 trang 67 Tập 1
Lời giải:
Gọi x (công nhân) là số công nhân thực hiện công việc dự định ban đầu.
Thời gian thực tế đội công nhân đó hoàn thiện công việc là:
12 + 6 = 18 (ngày).
Vì số công nhân và thời gian thực hiện công việc là hai đại lượng tỉ lệ nghịch nên 18x = 48 . 12 = 576.
Suy ra x = 576 : 18 = 32.
Do đó có 32 công nhân thực hiện công việc dự định ban đầu nên số công nhân bị điều động đi làm việc khác là:
48 – 32 = 16 (công nhân).
Vậy số công nhân bị điều động đi làm việc khác là 16 công nhân.
Lời giải:
Gọi x, y, z (học sinh) lần lượt là số học sinh tham dự thi của khối 6, 7, 8.
Theo đề bài, ba khối 6, 7, 8 có tất cả 200 học sinh tham dự thi nên
x + y + z = 200.
Ta có: hay
Suy ra: .
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
.
Do đó x = 13 . 5 = 65; y = 15 . 5 = 75; z = 12 . 5 = 60.
Vậy khối 6, 7, 8 lần lượt có: 65 học sinh, 75 học sinh, 60 học sinh tham dự cuộc thi.
Bài 91* trang 67 SBT Toán 7 Tập 1: Cho các số a, b, c thỏa mãn . Chứng tỏ rằng:
Lời giải:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
Suy ra hay c – a = –2(a – b) = –2(b – c).
Do đó (c – a)2 = [–2(a – b)][–2(b – c)] = 4(a – b)(b – c).
Vậy 4(a – b)(b – c) = (c – a)2.
Bài 92* trang 67 SBT Toán 7 Tập 1: Tìm giá trị nhỏ nhất của mỗi biểu thức sau:
b) với x ≥ 0.
Lời giải:
a) Ta có: |x − 1| ≥ 0 với mọi số thực x.
Nên A = |x − 1| + 21 ≥ 21 với mọi số thực x.
Vậy giá trị nhỏ nhất của A là 21. Dấu "=" xảy ra khi và chỉ khi |x − 1| = 0.
Suy ra x – 1 = 0 hay x = 1.
b) Ta có: , x2 ≥ 0 với mọi số thực x.
Nên với mọi số thực x.
Suy ra với mọi số thực x.
Vậy giá trị nhỏ nhất của B là –22.
Dấu "=" xảy ra khi và chỉ khi và x2 = 0. Suy ra x = 0.
Bài 93* trang 67 SBT Toán 7 Tập 1: Tìm giá trị lớn nhất của mỗi biểu thức sau:
a) C = − |x| − x2 + 23;
b) .
Lời giải:
a) Ta có: |x| ≥ 0, x2 ≥ 0 với mọi số thực x.
Nên − |x| − x2 ≤ 0 với mọi số thực x.
Suy ra C = − |x| − x2 + 23 ≤ 23 với mọi số thực x.
Vậy giá trị lớn nhất của C là 23.
Dấu "=" xảy ra khi và chỉ khi |x| = 0 và x2 = 0. Suy ra x = 0.
b) .
Ta có: x2 ≥ 0 với mọi số thực x.
Nên hay với mọi số thực x.
Suy ra hay D ≤ 1 220 với mọi số thực x.
Vậy giá trị lớn nhất của D là 1 220. Dấu "=" xảy ra khi và chỉ khi x2 = 0. Suy ra x = 0.
Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 1: Hình hộp chữ nhật. Hình lập phương
Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác




