Giải SBT Toán 6 (Kết nối tri thức) Bài tập ôn tập cuối năm

Sách bài tập Toán 6 Bài tập ôn tập cuối năm

Bài 1 trang 92 sách bài tập Toán 6 Tập 2 - KNTT: Theo các nhà khoa học, trong cơ thể người bình thường trung bình có khoảng 25 nghìn tỉ tế bào hồng cầu. Giả sử rằng tổng khối lượng hồng cầu này là 2,5 kg. Như vậy trong mỗi gam hồng cầu có bao nhiêu tế bào?

(Theo healthline.com)

Lời giải:

Số tế bào trong 1 gam hồng cầu = Tổng số tế bào : Khối lượng hồng cầu

Ta có: 1 tỉ = 1 000 triệu = 10³ . 10⁶ = 10⁹;

1 nghìn tỉ = 1 000 tỉ = 10³ . 10⁹ = 10¹².

Số lượng tế bào hồng cầu trong cơ thể người là: 2,5 kg = 25 . 10² g.

Số tế bào trong mỗi gam hồng cầu là:

25. 10¹² : (25 . 10²) = $\frac{25.{10}^2.{10}^{10}}{25.{10}^2}$ = 10¹⁰ (tế bào) = 10 tỉ (tế bào).

Vậy trong mỗi gam hồng cầu có 10 tỉ tế bào.

Bài 2 trang 92 sách bài tập Toán 6 Tập 2 - KNTT: Trên một tia số gốc O, ba điểm A, B và M lần lượt biểu diễn các số tự nhiên a, b và m. Hãy so sánh ba số a, b và m, biết rằng:

• Trong ba điểm A, B và M, điểm B nằm gần gốc O nhất;

• Điểm M nằm giữa hai điểm A và B.

Lời giải:

Vì ba điểm A, B và M lần lượt biểu diễn các số tự nhiên a, b và m nên OA = a, OB = b, OM = m.

Vì điểm B nằm gần gốc O nhất nên độ dài đoạn OB ngắn nhất hay b nhỏ nhất.

Mà điểm M nằm giữa hai điểm A và B, ba điểm này nằm cùng phía với điểm gốc O nên ta được: OB < OM < OA.

Vậy b < m < a.

Bài 3 trang 92 sách bài tập Toán 6 Tập 2 - KNTT: Vận dụng dấu hiệu chia hết cho 2, 3 và 5, em hãy phân tích các số sau ra thừa số nguyên tố.

a) 9 720;

b) 30 375.

Lời giải:

- Dấu hiệu chia hết cho 2: các số có chữ số tận cùng là 0; 2; 4; 6; 8.

- Dấu hiệu chia hết cho 5: các số có chữ số tận cùng là 0 hoặc 5.

- Dấu hiệu chia hết cho 3: các số có tổng các chữ số là một số chia hết cho 3.

a) Phân tích số 9 720 ra thừa số nguyên tố, ta được:

$\left.\begin{array}{l}9720\\ 4860\\ 2430\\ 1215\\ 405\\ 135\\ 45\\ 15\\ 5\\ 1\end{array}\right|\begin{array}{c}2\\ \begin{array}{l}2\\ 2\\ 3\\ 3\\ 3\\ 3\\ 3\\ 5\\ \end{array}\end{array}$

Vậy 9 720 = 2³ . 3⁵ . 5

b) Phân tích số 30 375 ra thừa số nguyên tố, ta được:

$\left.\begin{array}{l}30375\\ 10125\\ 3375\\ 1125\\ 375\\ 125\\ 25\\ 5\\ 1\end{array}\right|\begin{array}{c}3\\ \begin{array}{l}3\\ 3\\ 3\\ 3\\ 5\\ 5\\ 5\\ \end{array}\end{array}$

Vậy 30 375 = 3⁵ . 5³.

Bài 4 trang 92 sách bài tập Toán 6 Tập 2 - KNTT: Hai anh Hoàng và Hà thuê trọ ở cùng một nhà nhưng làm ở hai công ty khác nhau. Anh Hoàng cứ 15 ngày đi trực một lần, anh Hà cứ 20 ngày đi trực một lần. Hai anh cùng trực vào thứ Sáu ngày 1-1-2021. Hỏi trong năm 2021, hai anh sẽ cùng trực vào ngày thứ Sáu bao nhiêu lần?

Lời giải:

Gọi x là số ngày ngắn nhất để hai anh lại cùng trực một ngày (x > 0).

y là số ngày ngắn nhất để 2 anh lại cùng trực một ngày thứ Sáu (y > 0).

Ta có: x = BCNN (15; 20) = 60.

Khi đó, cứ sau 60 ngày thì hai anh lại trực cùng một ngày.

Ta lại có hai ngày thứ Sáu liên tiếp cách nhau 7 ngày nên:

y = BCNN (60; 7) = 420.

Khi đó cần 420 ngày, hai anh mới lại cùng trực một ngày thứ Sáu.

Tuy nhiên, năm 2021 có 365 ngày nên trong năm 2021.

Do đó, hai anh chỉ trực cùng nhau ngày vào một ngày thứ Sáu trong năm 2021.

Vậy hai anh chỉ trực cùng nhau vào thứ Sáu ngày 1-1-2021.

Bài 5 trang 92, 93 sách bài tập Toán 6 Tập 2 - KNTT: Trên một trục số gốc O, hai điểm A và B lần lượt biểu diễn hai số nguyên a và b.

a) Hãy tính khoảng cách AB trong mỗi trường hợp sau đây:

• a = 3 và b = 7;

• a = −3 và b = 7;

• a = −7 và b = −3;

b) Tại sao có thể kết luận rằng ta luôn có AB = b − a nếu a < b.

HD: Với mọi trường hợp sau, hãy vẽ hình minh họa (trên trục số nằm ngang với chiều dương từ trái sang phải) và chú ý rằng điểm biểu diễn số nguyên âm nằm cách gốc O một khoảng bằng −a (chẳng hạn điểm −3 nằm cách gốc O một khoảng bằng 3 = −(−3):

• Điểm O trùng với một trong hai điểm A và B.

• Điểm O nằm giữa hai điểm A và B.

• Điểm O nằm trước (bên phải) cả hai điểm A và B.

• Điểm O nằm sau (bên trái) cả hai điểm A và B.

Lời giải:

a) 

• a = 3 và b = 7

- Vẽ trục số nằm ngang gốc O.

- Hai điểm A và B lần lượt biểu diễn hai số nguyên a = 3 và b = 7.

Hai điểm A và B được biểu diễn trên trục số như hình vẽ:

Dựa trên hình vẽ, ta có: OA = 3, OB = 7.

Khoảng cách AB:

AB = OB – OA = 7 – 3 = 4

Vậy AB = 4.

• a = −3 và b = 7

- Vẽ một trục số gốc O.

- Hai điểm A và B lần lượt biểu diễn hai số nguyên a = −3 và b = 7.

Hai điểm A và B được biểu diễn trên trục số như hình vẽ:

Dựa trên hình vẽ, ta có: OA = 3, OB = 7.

Khoảng cách AB:

AB = OA + OB = 3 + 7 = 10

Vậy AB = 10.

• a = −7 và b = −3

- Vẽ một trục số gốc O.

- Hai điểm A và B lần lượt biểu diễn hai số nguyên a = −7 và b = −3

Hai điểm A và B được biểu diễn trên trục số như hình vẽ:

Ta có hình vẽ:

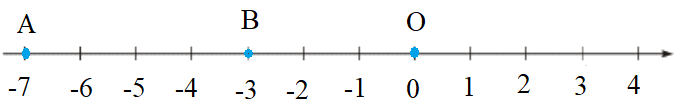
Dựa trên hình vẽ, ta có: OA = 7, OB = 3.

Khoảng cách AB:

AB = OA − OB = 7 − 3 = 4

Vậy AB = 4.

b) Hai điểm A và B lần lượt biểu diễn hai số nguyên a và b mà a < b.

Nên điểm A nằm bên trái điểm B trên trục số.

Ta xét các trường hợp sau:

• Điểm O trùng với một trong hai điểm A và B.

+ Điểm O trùng điểm A (như hình vẽ). Khi đó, a = 0.

Do đó: AB = OB = b = b – 0 = b – a.

+ Điểm O trùng điểm B. Khi đó, b = 0.

Suy ra: điểm A biểu diễn số nguyên âm nên OA = –a.

Do đó: AB = AO = OA = –a = 0 – a = b – a.

•  Điểm O nằm giữa A và B.

Khi đó, điểm A biểu diễn số nguyên âm nên OA = –a;

Điểm B biểu diễn số nguyên dương nên OB = b.

Vì điểm O nằm giữa hai điểm A và B nên:

AB = OB + OA = b + (–a) = b – a.

• Điểm O nằm trước (bên phải) cả hai điểm A và B.

Mà điểm A nằm bên trái điểm B trên trục số.

Nên diểm A nằm giữa O và B (như hình vẽ).

Khi đó, hai điểm A và B đều biểu diễn số nguyên dương.

Nên OA = a, OB = b.

Ta có A nằm giữa O và B nên AO + AB = OB

Do đó: AB = OB – AO = b – a.

• Điểm O nằm sau (bên trái) cả hai điểm A và B.

Mà điểm A nằm bên trái điểm B trên trục số.

Nên điểm B nằm giữa A và O (như hình vẽ).

Khi đó, hai điểm A và B đều biểu diễn số nguyên âm.

Nên OA = –a; OB = –b.

Vì B nằm giữa A và O nên AB + BO = AO.

Do đó: AB = AO – BO = –a – (–b) = b – a .

Vậy ta có thể kết luận rằng ta luôn có AB = b – a nếu a < b.

Bài 6 trang 93 sách bài tập Toán 6 Tập 2 - KNTT: Tính giá trị của biểu thức P = a . b – 3(17 – a + 2b) trong mỗi trường hợp sau:

a) a = 15 và b = –28;

b) a = –6 và b = 11;

c) a = –17 và b = –3.

Lời giải:

a) Thay a = 15 và b = –28  vào biểu thức P, ta được:

P = 15 . (–28) – 3 . [17 – 15 + 2 . (–28)]

= (–420) – 3 . [2 + (–56)]

= (–420) – 3 . (–54)

= (–420) + 162

= –258.

Vậy với a = 15 và b = –28 thì P = –258.

b) Thay a = –6 và b = 11 vào biểu thức P, ta được:

P = (–6) .11 – 3. [17 – (–6) + 2 . 11]

= (–66) – 3 . (17 + 6 + 22)

= (–66) – 3 . 45

= (–66) – 135

= –201.

Vậy với a = 15 và b = –28 thì P = –201.

c) Thay a = –6 và b = 11 vào biểu thức P, ta được:

P = (–17) . (–3) – 3. [17 – (–17) + 2 . (–3)]

= 17 . 3 – 3 . (17 + 17 – 6)

= 17 . 3 – 3 . 28

= 3 . (17 – 28)

= 3 . (–11)

= –33.

Vậy với a = –6 và b = 11 thì P = –33.

Bài 7 trang 93 sách bài tập Toán 6 Tập 2 - KNTT: Bạn Đông chơi trò chơi ném bi. Đích ném là một cái hộp có 25 ô. Điểm tính cho mỗi lần ném bi được quy định như sau:

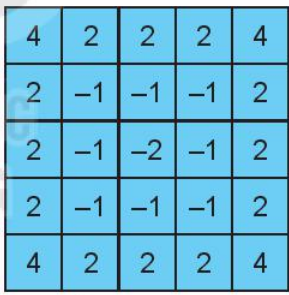
• Nếu ném ra ngoài hộp thì được tính là –5 điểm;

• Nếu ném vào một trong 25 ô trong hộp thì điểm tính được ghi như hình bên.

Trong 14 lần đầu, Đông ném 2 lần vào ô 4 điểm, 7 lần vào ô 2 điểm, 1 lần vào ô –2 điểm và 4 lần vào ô –1 điểm.

a) Viết biểu thức số biểu thị số điểm mà Đông có được sau lần ném bi thứ 14. Tính giá trị của biểu thức đó.

b) Đông còn một lần ném bi nữa. Hỏi Đông có cơ hội đạt được 20 điểm không? Nếu được thì lần cuối, Đông cần phải ném vào ô bao nhiêu điểm?

Lời giải:

a) Số điểm Đông có được khi ném 2 lần vào ô 4 điểm là:

2 . 4 = 8 (điểm)

Số điểm Đông có được khi ném 7 lần vào ô 2 điểm là:

7 . 2 = 14 (điểm)

Số điểm Đông có được khi ném 1 lần vào ô –2 điểm là:

1 . (–2) = –2 (điểm)

Số điểm Đông có được khi ném 4 lần vào ô –1 điểm là:

4 . (–1) = –4 (điểm)

Vậy biểu thức số biểu thị số điểm mà Đông có được sau lần ném bi thứ 14 bằng tổng số điểm của 14 lần ném đầu và bằng:

A = 2 . 4 + 7 . 2 + 1 . (–2) + 4 . (–1).

Giá trị của biểu thức A là: A = 8 + 14 + (–2) + (–4) = 16.

b) Để đạt được 20 điểm thì Đông còn thiếu số điểm là:

20 – 16 = 4 (điểm)

Vậy Đông vẫn còn cơ hội đạt được 20 điểm. Nếu được thì lần cuối Đông cần phải ném vào ô 4 điểm.

Bài 8 trang 93 sách bài tập Toán 6 Tập 2 - KNTT: Em hãy vẽ các hình sau:

a) Hình tam giác đều có cạnh dài 4 cm;

b) Hình vuông có cạnh dài 3 cm;

c) Hình chữ nhật có chiều dài bằng 5 cm, chiều rộng bằng 3 cm;

d) Hình bình hành có một cạnh dài 3 cm, một cạnh dài 5 cm.

Lời giải:

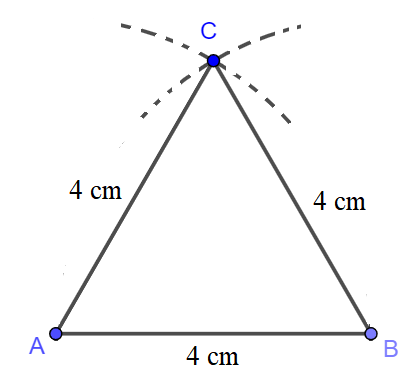
a) Tam giác đều có cạnh dài 4 cm, tức là ba cạnh của tam giác đều bằng 4 cm. Gọi tam giác đều cần vẽ là tam giác ABC.

* Cách vẽ hình tam giác đều có cạnh dài 4 cm:

- Vẽ đoạn thẳng AB = 4 cm.

- Dùng compa vẽ hai đường tròn (A; 4cm) và (B; 4cm).

- Hai đường tròn này cắt nhau tại điểm C.

Nối A với C, B với C. Ta được tam giác cần vẽ là tam giác đều có độ dài một cạnh bằng 4 cm.

* Ta có hình vẽ:

b) Gọi hình vuông cần vẽ là hình vuông ABCD.

* Cách vẽ hình vuông có cạnh dài 3 cm:

- Vẽ đoạn thẳng AB = 3 cm.

- Vẽ đường thẳng vuông góc với AB tại A. Xác định điểm D trên đường thẳng đó sao cho AD = 3 cm.

- Vẽ đường thẳng vuông góc với AB tại B. Xác định điểm C trên đường thẳng đó sao cho BC = 3 cm.

- Nối C với D ta được hình vuông ABCD cạnh bằng 3 cm.

* Ta có hình vẽ:

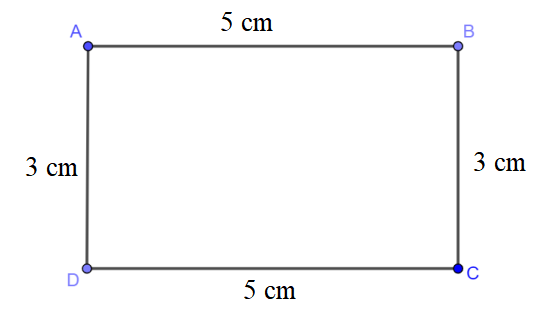
c) Gọi hình chữ nhật cần vẽ là hình chữ nhật ABCD có chiều dài AB = CD = 5 cm, AD = BC = 3 cm.

* Cách vẽ hình chữ nhật có chiều dài bằng 5 cm, chiều rộng bằng 3 cm:

- Vẽ đoạn thẳng AB = 5 cm.

- Vẽ đường thẳng vuông góc với AB tại A. Trên đường thẳng đó lấy điểm D sao cho AD = 3 cm.

- Vẽ đường thẳng vuông góc với AB tại B. Trên đường thẳng đó lấy điểm C sao cho BC = 3 cm.

- Nối D với C ta được hình chữ nhật ABCD.

* Ta có hình vẽ:

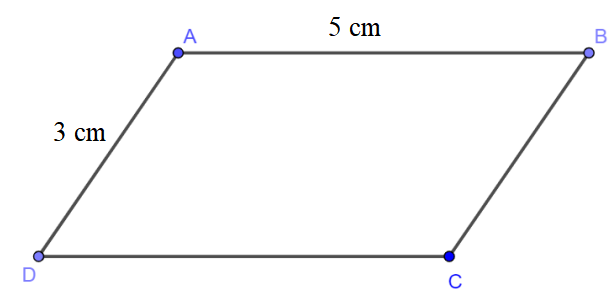
d) Gọi hình bình hành cần vẽ là hình bình hành ABCD có cạnh độ dài cạnh AB = CD = 5 cm (là cạnh đáy) và AD = BC = 3 cm (là cạnh bên).

* Cách vẽ hình bình hành có một cạnh dài 3 cm, một cạnh dài 5 cm:

- Vẽ đoạn thẳng AB = 5 cm.

- Vẽ đường thẳng đi qua B. Trên đường thẳng đó lấy điểm C sao cho BC = 3 cm.

- Vẽ đường thẳng đi qua A và song song với BC, đường thẳng qua C và song song với AB.

Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD.

* Ta có hình vẽ:

Bài 9 trang 94 sách bài tập Toán 6 Tập 2 - KNTT: Nền nhà của bác Thu có hình dạng và kích thước như hình vẽ bên:

a) Tính chu vi của nền nhà.
b) Bác Thu dự định dùng những viên gạch lát hình vuông có cạnh 50 cm để lát nền nhà. Hỏi bác Thu cần mua bao nhiêu viên gạch?

Lời giải:

a) Chu vi của nền nhà là:

8 + 10 + 6 + 2 = 36 (m)

b) Ta có thể vẽ thêm nét để tạo thành hình chữ nhật có chiều dài 10 m và chiều rộng 8 m (như hình vẽ).

Đổi 50 cm = 0,5 m

Diện tích hình chữ nhật mới là:

8 . 10 = 80 (m²)

Diện tích hình chữ nhật được tăng thêm sau khi vẽ là:

2 . 6 = 12 (m²)

Diện tích nền nhà là:

80 – 12 = 68 (m²)

Diện tích một viên gạch hình vuông cạnh 50 cm là:

0,5 . 0,5 = 0,25 (m²)

Số viên gạch Bác Thu cần mua để lát nền là:

68 : 0,25 = 272 (viên)

Vậy bác Thu cần mua 272 viên gạch để lát nền.

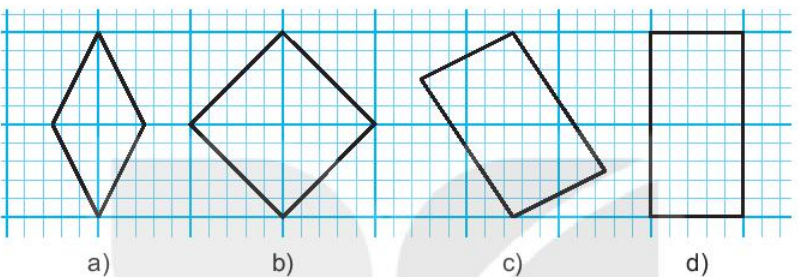
Bài 10 trang 94 sách bài tập Toán 6 Tập 2 - KNTT: Quan sát các hình dưới đây và trả lời các câu hỏi:

a) Những hình nào có tâm đối xứng?

b) Những hình nào có trục đối xứng?

c) Những hình nào có đúng hai trục đối xứng?

d) Những hình nào có nhiều hơn hai trục đối xứng?

Lời giải:

a) Những hình có tâm đối xứng:

- Hình a) có tâm đối xứng (như hình vẽ)

- Hình b) có tâm đối xứng (như hình vẽ)

- Hình c) có tâm đối xứng (như hình vẽ)

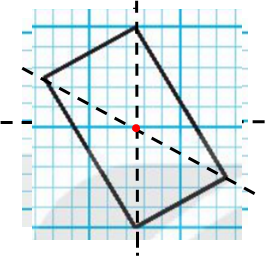
- Hình d) có tâm đối xứng (như hình vẽ)

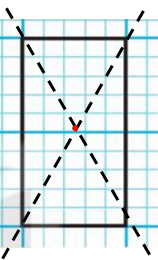
- Hình e) có tâm đối xứng (như hình vẽ)

- Hình f) có tâm đối xứng (như hình vẽ)

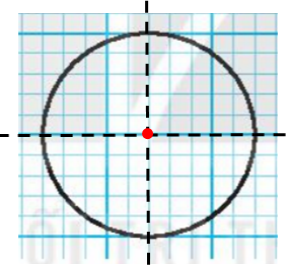
Vậy những hình có tâm đối xứng là: a, b, c, d, e, f.

b) Những hình có trục đối xứng:

- Hình a) có trục đối xứng (như hình vẽ).

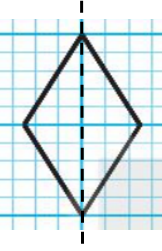
- Hình b) có trục đối xứng (như hình vẽ).

- Hình c) không có trục đối xứng.

- Hình d) có trục đối xứng (như hình vẽ)

- Hình e) có trục đối xứng (như hình vẽ)

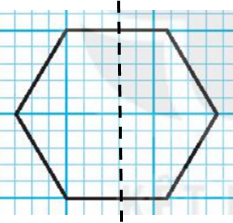
- Hình f) có tâm đối xứng (như hình vẽ)

- Hình g) có tâm đối xứng (như hình vẽ)

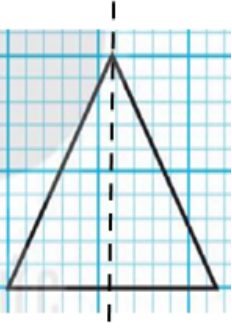
Vậy những hình có trục đối xứng là: a, b, d, e, f, g.

c) Những hình có hai trục đối xứng:

- Hình a) có hai trục đối xứng (như hình vẽ).

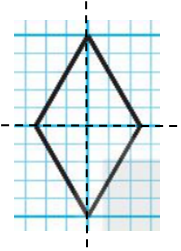
- Hình d) có hai trục đối xứng (như hình vẽ).

Vậy những hình có hai trục đối xứng là: a, d.

d) Những hình có nhiều hơn hai trục đối xứng:

- Hình b) có nhiều hơn hai trục đối xứng (như hình vẽ).

- Hình e) có nhiều hơn hai trục đối xứng (như hình vẽ)

- Hình f) có nhiều hơn hai tâm đối xứng (như hình vẽ)

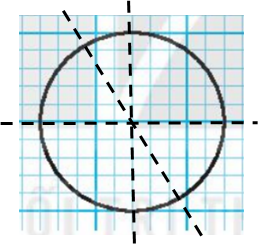
- Hình g) có nhiều hơn hai tâm đối xứng (như hình vẽ)

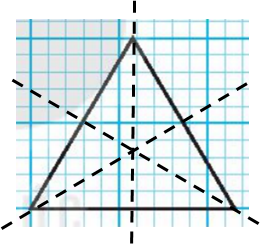
Vậy những hình có nhiều hơn hai trục đối xứng là: b, e, f, g.

Bài 11 trang 94 sách bài tập Toán 6 Tập 2 - KNTT: Em hãy vẽ hình sau vào vở. Trên hình vừa vẽ, hãy vẽ trục đối xứng của hình và vẽ thêm để được một hình có tâm đối xứng.

Lời giải:

Trục đối xứng là đường thẳng d (như hình vẽ).

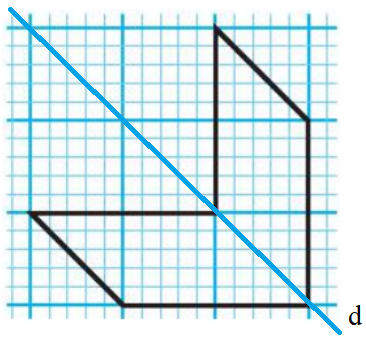
Ta có hình vẽ có tâm đối xứng:

 

Bài 12 trang 95 sách bài tập Toán 6 Tập 2 - KNTT: Em hãy phác họa bức hình sau vào vở và vẽ nốt nửa bên phải để được một hình nhận đường thẳng d là trục đối xứng.

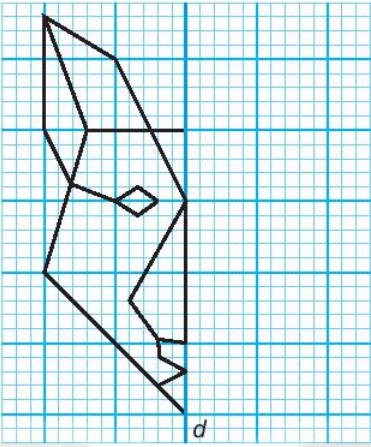
Lời giải:

* Cách vẽ:

- Xác định các điểm đối xứng với các đỉnh của hình ban đầu qua trục đối xứng d.

- Nối các điểm mới lại với nhau. Ta được hình cần vẽ.

Bài 13 trang 95 sách bài tập Toán 6 Tập 2 - KNTT: Trên quãng đường AB, hai xe cùng khởi hành một lúc. Xe tải đi từ A đến B hết 3 giờ, xe con đi từ B về A hết 2 giờ. Hỏi sau bao lâu thì hai xe gặp nhau?

Lời giải:

Xe tải đi hết quãng đường AB hết 3 giờ nên:

Trong 1 giờ, xe tải đi được $\frac{1}{3}$ quãng đường AB;

Xe con đi hết quãng đường AB hết 2 giờ nên:

Trong 1 giờ, xe con đi được $\frac{1}{2}$ quãng đường AB.

Như vậy,  trong 1 giờ cả hai xe đi được  $\frac{1}{3}+\frac{1}{2}=\frac{5}{6}$  quãng đường AB.

Hai xe gặp nhau sau khoảng thời gian là:

1 :  $\frac{5}{6}=\frac{6}{5}$  (giờ).

Ta có: $\frac{6}{5}$ giờ = $1\frac{1}{5}$ giờ = 1 giờ 12 phút.

Vậy sau 1 giờ 12 phút thì hai xe gặp nhau.

Bài 14 trang 95 sách bài tập Toán 6 Tập 2 - KNTT: Tính một cách hợp lí:

a) $A=\frac{-11}{13}+\frac{8}{19}+\left(-\frac{54}{13}\right)+\frac{1}{5}+\frac{11}{19}$

b) $B=\frac{17}{20}+\left(-\frac{8}{21}\right)+\left(-\frac{3}{4}\right)+\frac{29}{21}-\frac{37}{20}$

Lời giải:

a)$A=\frac{-11}{13}+\frac{8}{19}+\left(-\frac{54}{13}\right)+\frac{1}{5}+\frac{11}{19}$

 $=\frac{-11}{13}+\left(-\frac{54}{13}\right)+\frac{8}{19}+\frac{11}{19}+\frac{1}{5}$   (Tính chất giao hoán)

   $=\left(\frac{-11}{13}+\frac{-54}{13}\right)+\left(\frac{8}{19}+\frac{11}{19}\right)+\frac{1}{5}$       (Tính chất kết hợp)

$$\begin{gathered} =\frac{-65}{13}+\frac{19}{19}+\frac{1}{5} \\ =-5+1+\frac{1}{5} \\ =-4+\frac{1}{5} \\ =\frac{-19}{5} \end{gathered}$$

b) $B=\frac{17}{20}+\left(-\frac{8}{21}\right)+\left(-\frac{3}{4}\right)+\frac{29}{21}-\frac{37}{20}$

     $=\frac{17}{20}-\frac{37}{20}+\frac{-8}{21}+\frac{29}{21}+\frac{-3}{4}$    (Tính chất giao hoán)

$=\left(\frac{17}{20}-\frac{37}{20}\right)+\left(\frac{-8}{21}+\frac{29}{21}\right)+\frac{-3}{4}$ (Tính chất kết hợp)

$$\begin{gathered} =\frac{-20}{20}+\frac{21}{21}+\frac{-3}{4} \\ =-1+1+\frac{-3}{4} \\ =\frac{-3}{4} \end{gathered}$$

Bài 15 trang 95 sách bài tập Toán 6 Tập 2 - KNTT: Nhiệt độ không khí T (theo đơn vị độ C) bên ngoài máy bay ở độ cao h (theo đơn vị feet) được cho bởi công thức:

T = 26 − $\frac{h}{500}$.

Khi máy bay ở độ cao 10 000 m thì nhiệt độ bên ngoài máy bay là bao nhiêu độ C (làm tròn kết quả đến hàng đơn vị)?

Lời giải:

Ta có: 1 foot ≈ 0,3048 m.

Nên 1 m ≈ 1 : 0,3048 (feet)

Do đó, 10 000 m ≈ 10 000 : 0,3048 (feet)

Khi máy bay ở độ cao 10 000 m thì nhiệt độ bên ngoài máy bay là:

T = 26 −  = −39,61679…. (^oC)

Làm tròn số −39,61679…. đến chữ số hàng đơn vị, ta được −40.

Vậy khi máy bay ở độ cao 10 000 m thì nhiệt độ bên ngoài máy bay khoảng −40 độ C.

Bài 16 trang 95, 96 sách bài tập Toán 6 Tập 2 - KNTT: Thời gian t (tính bằng phút) của hiện tượng nguyệt thực toàn phần được cho bởi công thức gần đúng:

$t\approx \frac{Dk-Kd}{60K}$,

trong đó d và D lần lượt là đường kính (tính bằng kilômet) của Mặt Trăng và Mặt Trời; k và K lần lượt là khoảng cách (tính bằng kilômet) từ Trái Đất đến Mặt Trăng và Mặt Trời.

Sử dụng công thức trên hãy cho biết hiện tượng nguyệt thực toàn phần kéo dài trong bao lâu giây (làm tròn kết quả đến hàng phần trăm).

Cho biết: d = 3,48 . 10³ ; D = 1,41 . 10⁶ ; k = 3,82 . 10⁵ ; K = 1,48 . 10⁸.

Lời giải:

Thay d = 3,48 . 10³ ; D = 1,41 . 10⁶ ; k = 3,82 . 10⁵ ; K = 1,48 . 10⁸ vào biểu thức $\frac{Dk-Kd}{60K}$, ta được:

$\frac{1,41.{10}^6.3,82.{10}^5-1,48.{10}^8.3,48.{10}^3}{60.1,48.{10}^8}$

$$\begin{gathered} =\frac{5,3862.{10}^{11}-5,1504.{10}^{11}}{88,8.{10}^8} \\ =\frac{(5,3862-5,1504).{10}^{11}}{88,8.{10}^8} \end{gathered}$$

$=\frac{0,2358.{10}^3}{88,8}$≈ 2,65.

Ta có: 2,65 phút = 2 phút 39 giây.

Vậy hiện tượng nguyệt thực toàn phần kéo dài trong khoảng 2 phút 39 giây.

Bài 17 trang 96 sách bài tập Toán 6 Tập 2 - KNTT: Trong khoảng thời gian từ năm 1977 đến năm 1999, một tàu vũ trụ đi được 22 tỉ dặm trong vũ trụ (dặm là một đơn vị đo chiều dài của các nước nói tiếng Anh, 1 dặm = 1,609 344 km). Em hãy cho biết:

a) Mỗi ngày, tàu vũ trụ đi được bao nhiêu dặm?

b) Mỗi giờ, tàu vũ trụ đi được bao nhiêu dặm?

(Làm tròn kết quả đến chữ số thập phân thứ nhất).

Lời giải:

Trong khoảng thời gian từ năm 1977 đến năm 1999, có 22 năm, trong đó có 5 năm nhuận là 1980; 1984; 1988; 1992; 1996 và 17 năm không nhuận.

Nên tổng số ngày trong khoảng thời gian từ năm 1977 đến năm 1999 là:

22 . 365 + 5 = 8 035 (ngày)

a) Mỗi ngày, tàu vũ trụ đi được số dặm là:

22 . 10⁹ : 8 035 ≈ 2 738 021,1 (dặm)

Vậy mỗi ngày, tàu vũ trụ đi được 2 738 021,1 dặm.

b) Mỗi giờ, tàu vũ trụ đi được số dặm là:

2 738 021, 2 : 24 ≈ 114 084,2 (dặm)

Vậy mỗi giờ, tàu vũ trụ đi được 114 084,2 dặm.

Bài 18 trang 96 sách bài tập Toán 6 Tập 2 - KNTT: Cho đoạn thẳng AC dài 6 cm. Điểm B nằm giữa A và C sao cho BC = 4 cm.

a) Vẽ hình rồi tính độ dài đoạn thẳng AB;

b) Trên tia đối của tia BA,lấy điểm D sao cho BD = 6 cm. Hãy so sánh AB và CD.

Lời giải:

a) Cách vẽ:

- Vẽ đoạn thẳng AC = 6 cm;

- Trên đoạn thẳng AC, lấy điểm B sao cho BC = 4 cm.

Ta có hình vẽ:

Vì điểm B nằm giữa hai điểm A và C nên BA + BC = AC

AB + 4 = 6

AB = 6 − 4

AB = 2 (cm).

Vậy AB = 2 cm.

b) Vì điểm D nằm trên tia đối của tia BA nên hai điểm B và D nằm cùng phía đối với điểm B.

Trên tia BC lấy điểm D sao cho BD = 6 cm.

Điểm C nằm giữa hai điểm B và D vì:

+ Ba điểm B, C, D cùng nằm trên một đường thẳng;

+ BC < BD (4 cm < 6 cm)

Từ đó ta suy ra: BC + CD = BD

4 + CD = 6

CD = 6 − 4

CD = 2 (cm)

Ta thấy AB = CD = 2 cm.

Vậy AB = CD.

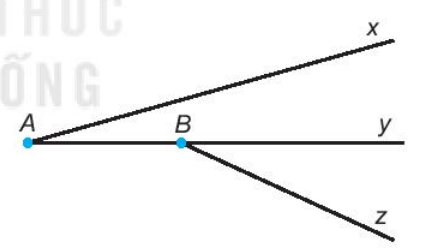
Bài 19 trang 96 sách bài tập Toán 6 Tập 2 - KNTT: Quan sát hình vẽ và trả lời câu hỏi:

a) Hai góc xAy và yBz có chung cạnh hay không?

b) Em nhận ra mấy cặp góc có chung cạnh? Hãy kể tên các cặp góc đó.

c) Trong hai góc xAy và yBz, góc nào lớn hơn (dùng thước đo góc để đo và trả lời)?

Lời giải:

a) Góc xAy có đỉnh là A và góc yBz có đỉnh là B.

Hai góc này có đỉnh khác nhau nên không chung cạnh.

Vậy hai góc xAy và yBz không chung cạnh.

b) Các cặp góc có chung cạnh là: 

+ $\widehat{ABy}$ và $\widehat{zBy}$(chung cạnh By);

+ $\widehat{zBy}$ và $\widehat{ABz}$ ( chung cạnh Bz);

+  $\widehat{ABz}$và $\widehat{ABy}$ (chung cạnh BA).

Vậy có 3 cặp góc có cạnh chung là $\widehat{ABy}$ và $\widehat{zBy}$, $\widehat{zBy}$và $\widehat{ABz}$, $\widehat{ABz}$ và $\widehat{ABy}$.

c) Đo hai góc $\widehat{xAy}$ và $\widehat{yBz}$, ta được:

$\widehat{xAy}$ = 15^o; $\widehat{yBz}$ = 25^o.

Do đó,$\widehat{yBz}$  > $\widehat{xAy}$ (25^o > 15^o).

 Vậy trong hai góc xAy và yBz thì góc yBz lớn hơn.

Bài 20 trang 96 sách bài tập Toán 6 Tập 2 - KNTT: Cho hình vẽ:

a) Hãy gọi tên các góc có đỉnh B trong hình.

b) Dùng êke hoặc thước đo góc kiểm tra và gọi tên góc vuông, góc tù có trong hình.

Lời giải:

a) Các cạnh có chứa đỉnh B là: BA, BH, BM, BC.

Lấy hai trong 4 cạnh trên sẽ tạo thành một góc.

Khi đó, các góc tạo thành là: $\widehat{ABH;}\widehat{ABC};\widehat{ABM};\widehat{CBM};\widehat{MBH};\widehat{CBH}$ .

Vậy các góc có đỉnh B trong hình là: $\widehat{ABH};\widehat{ABC};\widehat{ABM};\widehat{CBM};\widehat{MBH};\widehat{CBH}$ .

b)

* Dùng thước êke:

- Nếu hai cạnh của góc đó trùng với hai mép góc vuông của thước êke thì góc đó là vuông.

- Nếu góc đó có một phần thừa ra ngoài so với góc vuông của thước (hay nó lớn hơn góc vuông) thì góc đó là góc tù.

* Dùng thước đo góc: Đo các góc có trong hình rồi so sánh.

- Nếu góc có số đo bằng 90^o là góc vuông;

- Nếu góc có số đo nhỏ hơn 180^o và lớn hơn 90^o là góc tù.

Vậy trong hình trên có các góc vuông là: ;  và góc tù là: .

Bài 21 trang 97 sách bài tập Toán 6 Tập 2 - KNTT: Cho hình vẽ:

a) Đo và tính tổng số đo các góc của hình thoi OBCD.

b) Đo và tính tổng số đo các góc của tam giác AHB.

Lời giải:

a) Các góc của hình thoi OBCD là:$\widehat{OBC}; \widehat{BCD}; \widehat{ODC}; \widehat{BOD}$ .

Đo các góc của hình thoi, ta được:

$\widehat{OBC}=\widehat{ODC}$ = 60^o ;  $\widehat{BCD}=\widehat{BOD}$  = 120^o.

Tổng số đo các góc của hình thoi OBCD là:

60^o + 60^o + 120^o + 120^o  = 360^o .

Vậy số đo của các góc của hình thoi OBCD là $\widehat{OBC}=\widehat{ODC}$  = 60^o ;  $\widehat{BCD}=\widehat{BOD}$= 120^o  và tổng số đo của các góc đó là 360^o.

b) Các góc của tam giác AHB là: $\widehat{AHB}$;$\widehat{BAH}$ ; $\widehat{ABH}$.

Đo các góc của tam giác AHB, ta được:

 $\widehat{AHB}$= 90^o ; $\widehat{BAH}$ = 60^o ; $\widehat{ABH}$ = 30^o.

Tổng số đo các góc của tam giác AHB là:

90^o + 60^o + 30^o  = 180^o.

Vậy số đo các góc của tam giác AHB là $\widehat{AHB}$ = 90^o ; $\widehat{BAH}$ = 60^o ; $\widehat{ABH}$ = 30^o và tổng số đo các góc đó là 180^o.

Bài 22 trang 97 sách bài tập Toán 6 Tập 2 - KNTT: Trang và Hùng đã quan sát và ghi lại một số loại rác thải mà hai bạn gặp ở trên đường đi học gồm:

Quả táo, túi nylon (ni lông), vỏ bao thuốc lá, cốc thủy tinh, vỏ trứng, lá cây, thức ăn thừa, chai nhựa, đồ gốm sứ, bã trà, hộp giấy.

a) Hãy giúp Trang và Hùng phân loại các loại rác thải trên theo gợi ý sau:

b) Lập bảng thống kê cho biết số lượng mỗi loại rác thải từ bảng trên.

c) Vẽ biểu đồ cột biểu diễn bảng thống kê thu được ở câu b.

Lời giải:

a) Phân loại các loại rác thải trên vào 3 loại như sau:

- Loại rác dễ phân hủy: thức ăn thừa, quả táo, lá cây, bã trà, vỏ trứng;

- Loại rác tái chế: hộp giấy, vỏ bao thuốc lá, chai nhựa;

- Loại rác khó phân hủy: túi nylon, cốc thủy tinh, đồ gốm sứ.

Vậy ta có bảng phân loại sau:

Rác dễ phân hủy	Rác tái chế	Rác khó phân hủy
Thức ăn thừa, quả táo, lá cây, bã trà, vỏ trứng	Hộp giấy, vỏ bao thuốc lá, chai nhựa	Túi nylon, cốc thủy tinh, đồ gốm sứ

b) Số lượng mỗi loại rác thải trong bảng (câu a) ta có: rác thải dễ phân hủy là 5, rác tái chế là 3 và rác khó phân hủy là 3.

Từ đó ta có bảng thống kê số lượng mỗi loại rác thải như sau:

Loại rác	Rác dễ phân hủy	Rác tái chế	Rác khó phân hủy
Số lượng	5	3	3

c) Các bước vẽ biểu đồ cột:

Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau.

- Trục ngang ghi danh sách các loại rác thải: rác thải dễ phân hủy, rác tái chế và rác thải khó phân hủy.

- Trục dọc: căn cứ vào giá trị lớn nhất và nhỏ nhất, ta chia các khoảng cách đều nhau và đều bằng 1.

Bước 2: Tại vị trí các đối tượng trên trục ngang, vẽ các cột hình chữ nhật:

- Cách đều nhau;

- Có cùng chiều rộng;

- Có chiều cao thể hiện số lượng của các loại rác thải, tương ứng với khoảng chia  trên trục dọc.

Bước 3: Hoàn thiện biểu đồ.

- Ghi tên biểu đồ: Biểu đồ phân loại rác thải.

- Ghi tên các trục và số liệu tương ứng trên mỗi cột:

+ Trục ngang: loại rác;

+ Trục dọc: số lượng các loại rác. 

* Ta có biểu đồ số lượng mỗi loại rác thải như sau:

Bài 23 trang 97 sách bài tập Toán 6 Tập 2 - KNTT: Bảng thống kê sau đây cho biết điểm thi của An trong hai lần thi kết thúc học kì I và II.

a) Vẽ biểu đồ cột kép biểu diễn bảng thống kê trên.

b) Cho biết điểm thi của những môn nào tăng lên trong học kì II?

Lời giải:

a) Các bước vẽ biểu đồ cột kép:

Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau

- Trục ngang ghi danh sách các môn học: Toán, Ngữ văn và Khoa học tự nhiên.

- Trục dọc: Căn cứ vào giá trị lớn nhất và nhỏ nhất, ta chia các khoảng cách đều nhau và đều bằng 2.

Bước 2: Tại vị trí từng đối tượng trên trục ngang, vẽ 2 cột hình chữ nhật:

- Cách đều nhau;

- Có cùng chiều rộng;

- Có chiều cao thể hiện số điểm của các môn học, tương ứng với khoảng chia trên trục dọc.

Bước 3: Hoàn thiện biểu đồ.

- Tô màu hoặc gạch chéo để phân biệt hai cột trong cột kép

- Ghi tên biểu đồ: Điểm thi học kỳ của An.

- Ghi tên các trục và số liệu tương ứng trên mỗi cột:

+ Trục ngang: Môn học;

+ Trục dọc: Số điểm.

* Ta được biểu đồ cột kép biểu diễn bảng thống kê trên:

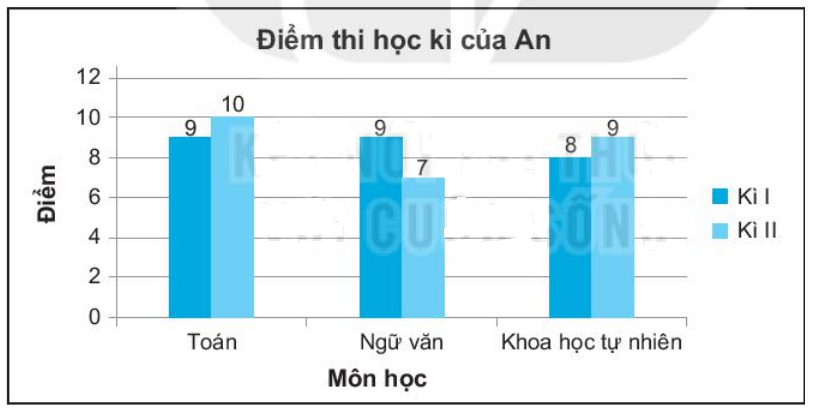
b) So sánh chiều cao cột bên trái (học kì I) và bên phải (học kì II) các môn của An, ta thấy:

- Môn toán: cột bên phải cao hơn cột bên trái nên điểm thi môn toán của An tăng lên trong học kì II.

- Môn Ngữ văn: cột bên phải thấp hơn cột bên trái nên điểm thi môn toán của An giảm đi trong học kì II.

- Môn Khoa học tự nhiên: cột bên phải cao hơn cột bên trái nên điểm thi môn Khoa học tự nhiên của An tăng lên trong học kì II.

Vậy điểm thi môn Toán và Khoa học tự nhiên của An tăng lên trong học kì II.

Bài 24 trang 97 sách bài tập Toán 6 Tập 2 - KNTT: Cô giáo chia lớp thành ba nhóm để thực hiện ba bài tập lớn bằng cách yêu cầu mỗi bạn chọn ngẫu nhiên một thẻ từ hộp kín chứa các thẻ ghi số 1; 2; 3. Các bạn chọn được thẻ ghi cùng số sẽ ở cùng một nhóm.

a) Em có thể thuộc nhóm nào?

b) Hãy xác định xem sự kiện “Em và Bình không cùng nhóm” có xảy ra không trong mỗi trường hợp sau:

- Em chọn được thẻ ghi số 1, Bình chọn được thẻ ghi số 3.

- Em chọn được thẻ ghi số 2, Bình chọn được thẻ ghi số 2.

Lời giải:

a) Thẻ em chọn có thể ghi số 1, số 2 hoặc số 3.

Các thẻ có cùng số sẽ ở cùng một nhóm.

Vậy em có thể thuộc nhóm 1 hoặc nhóm 2 hoặc nhóm 3.

b)     

- Khi em chọn được thẻ ghi số 1, Bình chọn được thẻ ghi số 3 thì em và Bình không cùng nhóm.

Vậy sự kiện “Em và Bình không cùng nhóm” xảy ra.

- Khi em chọn được thẻ ghi số 2, Bình chọn được thẻ ghi số 2 thì em và Bình cùng nhóm.

Vậy sự kiện “Em và Bình không cùng nhóm” không xảy ra.

Xem thêm các bài giải SBT Toán 6 Kết nối tri thức hay, chi tiết khác:

Bài 40. Biểu đồ cột

Bài 41. Biểu đồ cột kép

Bài 42. Kết quả có thể và sự kiện trong trò chơi, thí nghiệm

Bài 43. Xác suất thực nghiệm

Ôn tập chương 9