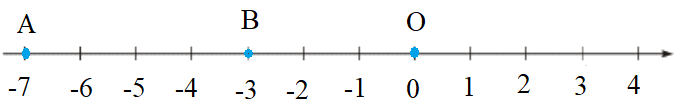Trên một trục số gốc O, hai điểm A và B lần lượt biểu diễn hai số nguyên a và b
159
31/12/2023
Bài 5 trang 92, 93 sách bài tập Toán 6 Tập 2 - KNTT: Trên một trục số gốc O, hai điểm A và B lần lượt biểu diễn hai số nguyên a và b.
a) Hãy tính khoảng cách AB trong mỗi trường hợp sau đây:
• a = 3 và b = 7;
• a = −3 và b = 7;
• a = −7 và b = −3;
b) Tại sao có thể kết luận rằng ta luôn có AB = b − a nếu a < b.
HD: Với mọi trường hợp sau, hãy vẽ hình minh họa (trên trục số nằm ngang với chiều dương từ trái sang phải) và chú ý rằng điểm biểu diễn số nguyên âm nằm cách gốc O một khoảng bằng −a (chẳng hạn điểm −3 nằm cách gốc O một khoảng bằng 3 = −(−3):
• Điểm O trùng với một trong hai điểm A và B.
• Điểm O nằm giữa hai điểm A và B.
• Điểm O nằm trước (bên phải) cả hai điểm A và B.
• Điểm O nằm sau (bên trái) cả hai điểm A và B.
Trả lời
a)
• a = 3 và b = 7
- Vẽ trục số nằm ngang gốc O.
- Hai điểm A và B lần lượt biểu diễn hai số nguyên a = 3 và b = 7.
Hai điểm A và B được biểu diễn trên trục số như hình vẽ:

Dựa trên hình vẽ, ta có: OA = 3, OB = 7.
Khoảng cách AB:
AB = OB – OA = 7 – 3 = 4
Vậy AB = 4.
• a = −3 và b = 7
- Vẽ một trục số gốc O.
- Hai điểm A và B lần lượt biểu diễn hai số nguyên a = −3 và b = 7.
Hai điểm A và B được biểu diễn trên trục số như hình vẽ:

Dựa trên hình vẽ, ta có: OA = 3, OB = 7.
Khoảng cách AB:
AB = OA + OB = 3 + 7 = 10
Vậy AB = 10.
• a = −7 và b = −3
- Vẽ một trục số gốc O.
- Hai điểm A và B lần lượt biểu diễn hai số nguyên a = −7 và b = −3
Hai điểm A và B được biểu diễn trên trục số như hình vẽ:
Ta có hình vẽ:
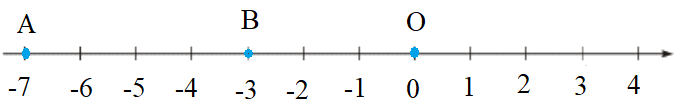
Dựa trên hình vẽ, ta có: OA = 7, OB = 3.
Khoảng cách AB:
AB = OA − OB = 7 − 3 = 4
Vậy AB = 4.
b) Hai điểm A và B lần lượt biểu diễn hai số nguyên a và b mà a < b.
Nên điểm A nằm bên trái điểm B trên trục số.
Ta xét các trường hợp sau:
• Điểm O trùng với một trong hai điểm A và B.
+ Điểm O trùng điểm A (như hình vẽ). Khi đó, a = 0.

Do đó: AB = OB = b = b – 0 = b – a.
+ Điểm O trùng điểm B. Khi đó, b = 0.

Suy ra: điểm A biểu diễn số nguyên âm nên OA = –a.
Do đó: AB = AO = OA = –a = 0 – a = b – a.
• Điểm O nằm giữa A và B.

Khi đó, điểm A biểu diễn số nguyên âm nên OA = –a;
Điểm B biểu diễn số nguyên dương nên OB = b.
Vì điểm O nằm giữa hai điểm A và B nên:
AB = OB + OA = b + (–a) = b – a.
• Điểm O nằm trước (bên phải) cả hai điểm A và B.
Mà điểm A nằm bên trái điểm B trên trục số.
Nên diểm A nằm giữa O và B (như hình vẽ).

Khi đó, hai điểm A và B đều biểu diễn số nguyên dương.
Nên OA = a, OB = b.
Ta có A nằm giữa O và B nên AO + AB = OB
Do đó: AB = OB – AO = b – a.
• Điểm O nằm sau (bên trái) cả hai điểm A và B.
Mà điểm A nằm bên trái điểm B trên trục số.
Nên điểm B nằm giữa A và O (như hình vẽ).

Khi đó, hai điểm A và B đều biểu diễn số nguyên âm.
Nên OA = –a; OB = –b.
Vì B nằm giữa A và O nên AB + BO = AO.
Do đó: AB = AO – BO = –a – (–b) = b – a .
Vậy ta có thể kết luận rằng ta luôn có AB = b – a nếu a < b.
Xem thêm các bài giải SBT Toán 6 Kết nối tri thức hay, chi tiết khác:
Bài 40. Biểu đồ cột
Bài 41. Biểu đồ cột kép
Bài 42. Kết quả có thể và sự kiện trong trò chơi, thí nghiệm
Bài 43. Xác suất thực nghiệm
Ôn tập chương 9
Bài tập ôn tập cuối năm