Sách bài tập Toán lớp 11 Bài 23: Đường thẳng vuông góc với mặt phẳng
Lời giải:
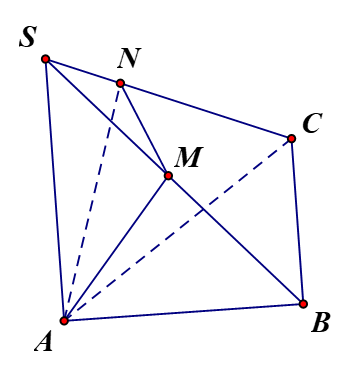
a) Vì SA ⊥ (ABC) nên SA ⊥ BC mà AB ⊥ BC (do tam giác ABC vuông tại B). Do đó BC ⊥ (SAB).
b) Vì BC ⊥ (SAB) nên BC⊥ AM, mà AM ⊥ SB (giả thiết). Do đó AM ⊥ (SBC).
c) Vì AM ⊥ (SBC) nên AM ⊥ SC, mà AN ⊥ SC (giả thiết). Do đó SC ⊥ (AMN).
b) H là trực tâm của tam giác ABC;
Lời giải:
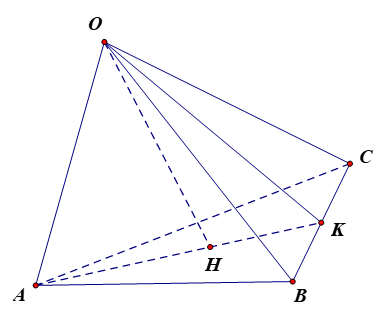
a) Vì OA ⊥ OB, OA ⊥ OC nên OA ⊥ (OBC). Suy ra OA ⊥ BC.
Mà OH ⊥ (ABC) nên OH ⊥ BC. Do đó BC ⊥ (OAH).
b) Vì BC ⊥ (OAH) nên BC ⊥ AH, do đó AH là đường cao của tam giác ABC. (1)
Có OH ⊥ (ABC) nên OH ⊥ AC.
Có OB ⊥ OA, OC ⊥ OB nên OB ⊥ (OAC) nên OB ⊥ AC mà OH ⊥ AC, từ đó suy ra AC ⊥ (OBH), suy ra CA ⊥ BH, do đó BH là đường cao của tam giác ABC. (2)
Từ (1) và (2) suy ra H là giao hai đường cao của tam giác ABC.
Do đó H là trực tâm của tam giác ABC.
c) Gọi K là giao điểm của AH với BC.
Vì OA ⊥ (OBC) nên OA ⊥ OK .
Xét tam giác OAK vuông tại O, có OH là đường cao nên 1OH2=1OA2+1OK2 .
Vì AK ⊥ BC mà OA ⊥ BC nên BC ⊥ (OAK), suy ra OK ⊥ BC.
Xét tam giác OBC vuông tại O, có OK là đường cao nên 1OK2=1OB2+1OC2 .
Do đó 1OH2=1OA2+1OB2+1OC2 .
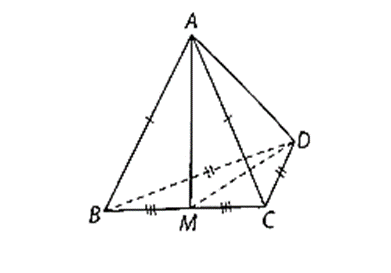
Bài 7.8 trang 28 SBT Toán 11 Tập 2: Cho tứ diện ABCD có AB = AC và DB = DC. Chứng minh rằng AD ⊥ BC.
Lời giải:
Gọi M là trung điểm của BC.
Xét tam giác ABC có AB = AC và AM là trung tuyến nên AM là đường cao.
Do đó AM ⊥ BC. (1)
Xét tam giác BCD có DC = DB và DM là trung tuyến nên DM là đường cao.
Do đó DM ⊥ BC. (2)
Từ (1) và (2) có: BC ⊥ (ADM). Suy ra BC ⊥ AD.
Lời giải:
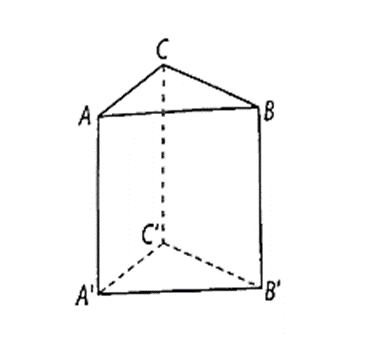
a) Vì AA' // BB'; AA' ⊥ (ABC) và (ABC) // (A'B'C') nên BB' ⊥ (A'B'C').
b) Vì BC ⊥ AB (do tam giác ABC vuông tại B).
Vì AA' // BB'; AA' ⊥ (ABC) nên BB' ⊥ (ABC), suy ra BC ⊥ BB' mà BC ⊥ AB nên BC ⊥ (ABB'A').
Lại có BC // B'C' nên B'C' ⊥ (ABB'A').
Lời giải:
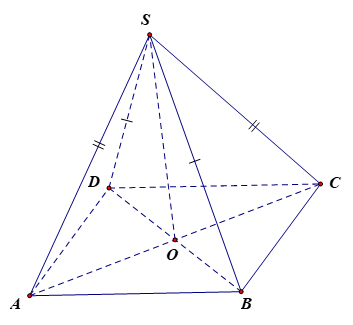
a)
Vì ABCD là hình thoi, O là giao điểm của AC và BD nên O là trung điểm của AC, BD.
Xét tam giác SAC có SA = SC, SO là trung tuyến nên SO là đường cao hay SO ⊥ AC.
Xét tam giác SBD có SB = SD, SO là trung tuyến nên SO là đường cao hay SO ⊥ BD.
Do đó SO ⊥ (ABCD).
b) Do ABCD là hình thoi nên AC ⊥ BD. (1)
Mà SO ⊥ (ABCD) nên AC ⊥ SO (2) và BD ⊥ SO (3).
Từ (1) và (2), suy ra AC ⊥ (SBD).
Từ (1) và (3), suy ra BD ⊥ (SAC).
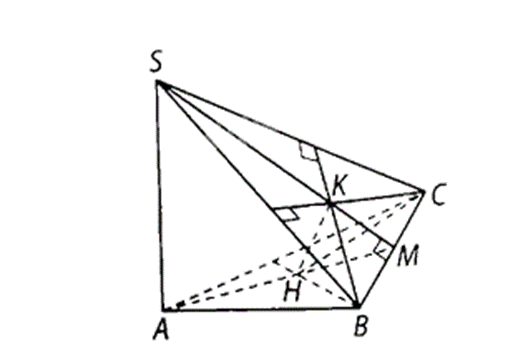
a) BC ⊥ (SAH) và các đường thẳng AH, BC, SK đồng quy;
Lời giải:
a) Vì H là trực tâm tam giác ABC nên BC ⊥ AH,
mà SA ⊥ (ABC) nên SA ⊥ BC. Do đó BC ⊥ (SAH).
Gọi M là giao điểm của AH và BC, ta có BC ⊥ (SAM) nên BC ⊥ SM.
Mặt khác, K là trực tâm của tam giác SBC nên SM đi qua K.
Do đó AH, BC, SK đồng quy.
b) Vì SA ⊥ (ABC) nên SA ⊥ CH, mà CH ⊥ AB, suy ra CH ⊥ (SAB).
Do đó CH ⊥ SB.
Lại có SB ⊥ CK nên SB ⊥ (CHK).
Xét tam giác SBC, K là trực tâm nên BK ⊥ SC.
Vì SA ⊥ (ABC) nên SA ⊥ BH mà BH ⊥ CA nên BH ⊥ (SAC), suy ra BH ⊥ SC.
Vì BK ⊥ SC và BH ⊥SC nên SC ⊥ (BHK), suy ra SC ⊥ HK.
Mà SB ⊥ HK (vì SB ⊥ (CHK)). Do đó HK ⊥ (SBC).
Lời giải:
Vì dây dọi song song với cây cột và dây dọi vuông góc với mặt phẳng sàn nên cây cột vuông góc với mặt phẳng sàn.
Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: