Giải SBT Toán 11 (Kết nối tri thức) Bài 22: Hai đường thẳng vuông góc

Sách bài tập Toán lớp 11 Bài 22: Hai đường thẳng vuông góc

Bài 7.1 trang 25 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, tam giác SAD là tam giác đều và M là trung điểm của cạnh AD. Tính góc giữa hai đường thẳng BC và SA; BC và SM.

Lời giải:

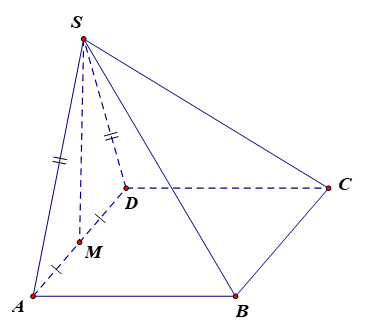
Vì ABCD là hình bình hành nên BC // AD. Do đó (BC, SA) = (AD, SA) = $\widehat{SAD}$.

Do tam giác SAD đều nên $\widehat{SAD}$ = 60^o .

Vậy góc giữa hai đường thẳng BC và SA bằng 60°.

Vì ABCD là hình bình hành nên BC // AD. Do đó (BC, SM) = (AD, SM).

Vì M là trung điểm của AD nên SM là đường trung tuyến.

Xét tam giác đều SAD có SM là đường trung tuyến nên SM là đường cao.

Do đó SM $\perp$ AD hay (AD, SM) = 90°.

Vậy góc giữa hai đường thẳng BC và SM bằng 90°.

Bài 7.2 trang 26 SBT Toán 11 Tập 2: Cho hình hộp ABCD.A'B'C'D' có tất cả các cạnh bằng nhau và góc A'AD bằng 120°. Tính góc giữa các cặp đường thẳng sau: A'C' và BD; AD và BB'; A'D và BB'.

Lời giải:

Vì hình hộp ABCD.A'B'C'D' có tất cả các cạnh bằng nhau nên ABCD là hình thoi, suy ra AC $\perp$ BD.

Mà A'C' // AC nên (A'C', BD) = (AC, BD) = 90°.

Vậy góc giữa hai đường thẳng A'C' và BD bằng 90°.

Vì BB' // AA' nên (AD, BB') = (AD, AA') = 180^o - $\widehat{A\text{'}AD}$ = 180^o - 120^o = 60^o.

Vậy góc giữa hai đường thẳng AD và BB' bằng 60°.

Vì BB' // AA' nên (A'D, BB') = (A'D, AA') = $\widehat{A\text{'}AD}$ .

Vì hình hộp ABCD.A'B'C'D' có tất cả các cạnh bằng nhau nên ADD'A' là hình thoi, suy ra A'D là đường phân giác của góc AA'D'.

Xét hình thoi ADD'A' có $\widehat{A\text{'}AD}$ = 120^o nên $\widehat{AA\text{'}D\text{'}}$ = 180^o - 120^o = 60^o.

Mà A'D là đường phân giác của góc AA'D' nên $\widehat{A\text{'}AD}$ = $\frac{{60}^o}{2}$ = 30^o.

Vậy góc giữa hai đường thẳng A'D và BB' bằng 30°.

Bài 7.3 trang 26 SBT Toán 11 Tập 2: Cho tứ diện ABCD, gọi M là N lần lượt là trung điểm của AC và BD. Biết MN = a$\sqrt{3}$; AB = 2$\sqrt{2}$a và CD = 2a. Chứng minh rằng đường thẳng AB vuông góc với đường thẳng CD.

Lời giải:

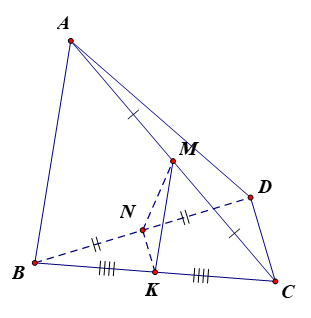
Lấy K là trung điểm của BC.

Xét tam giác BCD có N là trung điểm BD, K là trung điểm BC nên NK là đường trung bình. Do đó NK // CD và NK = $\frac{DC}{2}$ = a.

Xét tam giác ABC có M là trung điểm AC, K là trung điểm BC nên MK là đường trung bình. Do đó MK // AB và MK = $\frac{AB}{2}$ = $\sqrt{2}$a.

Có MN² = 3a² ; NK² + MK² = a² + ${\left(\sqrt{2a}\right)}^2$ = 3a².

Do đó MN² = NK² + MK² nên tam giác MNK là tam giác vuông tại K hay NK $\perp$ MK.

Lại có MK // AB, NK // CD nên (AB, CD) = (MK, NK) = 90° hay AB $\perp$ CD.

Bài 7.4 trang 26 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông tâm O và tất cả các cạnh của hình chóp đều bằng a. Gọi M, N lần lượt là trung điểm của cạnh SA, AB.

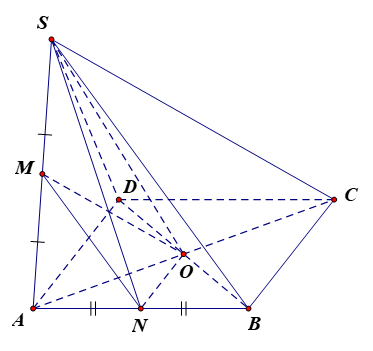
a) Tính góc giữa các cặp đường thẳng sau: MN và SD; MO và SB.

b) Tính tang của góc giữa hai đường thẳng SN và BC.

Lời giải:

a) Hình chóp S.ABCD có tất cả các cạnh bằng a và đáy ABCD là hình vuông nên

SA = SB = SC = SD = AB = BC = CD = DA = a.

Xét tam giác ADB vuông tại A, có BD² = AD² + AB² = a² + a² = 2a².

Mà SB² + SD² = a² + a² = 2a². Do đó SB² + SD² = BD² nên tam giác SBD vuông tại S.

Vì M, N lần lượt là trung điểm của cạnh SA, AB nên MN là đường trung bình của tam giác SAB, do đó MN // SB.

Khi đó (MN, SD) = (SB, SD) = 90°.

Vì O là giao điểm của AC và BD, ABCD là hình vuông nên O là trung điểm AC, BD.

Xét tam giác SAC có M là trung điểm SA, O là trung điểm AC nên MO là đường trung bình, suy ra MO // SC.

Khi đó (MO, SB) = (SC, SB) = $\widehat{BSC}$ = 60^o (do tam giác SBC là tam giác đều).

b) Xét tam giác ABC có O là trung điểm AC, N là trung điểm AB nên ON là đường trung bình, suy ra ON // BC.

Vì ON // BC nên (SN, BC) = (SN, ON) = $\widehat{SNO}$ .

Vì tam giác SAC có SA = SC = a nên tam giác SAC cân tại S mà SO là trung tuyến nên SO là đường cao.

Vì BD² = 2a² và ABCD là hình vuông nên AC = BD = a$\sqrt{2}$ $\Rightarrow$ AO = OC = $\frac{a\sqrt{2}}{2}$ .

Xét tam giác SOC vuông tại O, có:

SC² = SO² + OC² $\iff$a² = SO² + ${\left(\frac{a\sqrt{2}}{2}\right)}^2\iff$SO = $\frac{a\sqrt{2}}{2}$.

Vì ON là đường trung bình của tam giác ABC nên ON = $\frac{BC}{2}=\frac{a}{2}$.

Xét tam giác đều SAB có SN là trung tuyến đồng thời là đường cao hay SN $\perp$ AB.

Xét tam giác vuông SNB vuông tại N, ta có:

SN² + NB² = SB² $\iff$ SN² + ${\left(\frac{a}{2}\right)}^2$ = a² $\iff$ SN² = $\frac{3a^2}{4}$

Lại có SO² + ON² = ${\left(\frac{a\sqrt{2}}{2}\right)}^2$+ ${\left(\frac{a}{2}\right)}^2$ = $\frac{3a^2}{4}$ . Do đó tam giác SON vuông tại O.

Xét tam giác vuông SON vuông tại O có tan$\widehat{SNO}$ = $\frac{SO}{ON}$ = $\sqrt{2}$.

Vậy tang của góc giữa hai đường thẳng SN và BC là $\sqrt{2}$ .

Bài 7.5 trang 26 SBT Toán 11 Tập 2: Một chiếc thang có dạng hình thang cân cao 6 m, hai chân thang cách nhau 80 cm, hai ngọn thang cách nhau 60 cm. Thang được dựa vào bờ tường như hình bên. Tính góc tạo giữa đường thẳng chân tường và cạnh cột thang (tính gần đúng theo đơn vị độ, làm tròn kết quả đến chữ số thập phân thứ hai).

Lời giải:

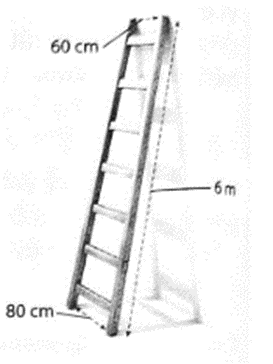
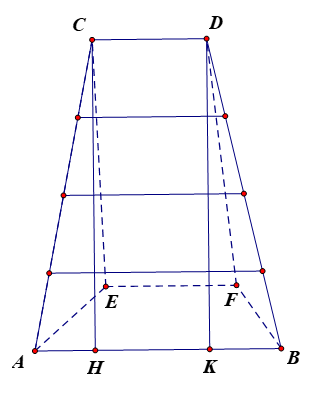
Gọi A, B là hai điểm tại hai vị trí chân thang và C, D là hai điểm tại hai vị trí ngọn thang, EF là đường chân tường.

Ta có EF // AB nên (EF, AC) = (AB, AC) = $\widehat{BAC}$ .

Kẻ CH $\perp$ AB tại H, DK $\perp$ AB tại K.

Ta có CDKH là hình chữ nhật nên CH = DK, CD = HK.

Xét $∆$CHA và $∆$DKB có

CA = DB, $\widehat{CHA}=\widehat{DKB}$ = 90^o , CH = DK nên $∆$CHA = $∆$DKB (c – g – c).

Suy ra AH = KB.

Khi đó AH = $\frac{AB-CD}{2}$ = 10 (cm) = 0,1 (m).

Vì tam giác ACH vuông tại H nên cos$\widehat{CAH}=\frac{AH}{AC}=\frac{0,1}{6}=\frac{1}{60}\Rightarrow \widehat{CAH}\approx$ 89,05^o.

Do đó, $\widehat{BAC}\approx$ 89,05^o.

Vậy góc tạo giữa đường thẳng chân tường và cạnh cột thang khoảng 89,05°.

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: