Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, tam giác SAD là tam giác đều

Bài 7.1 trang 25 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, tam giác SAD là tam giác đều và M là trung điểm của cạnh AD. Tính góc giữa hai đường thẳng BC và SA; BC và SM.

Trả lời

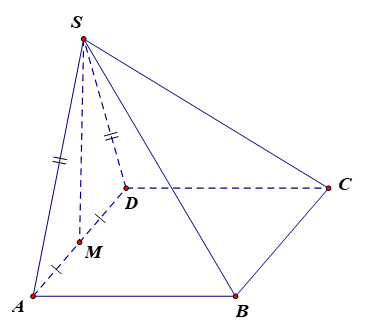
Vì ABCD là hình bình hành nên BC // AD. Do đó (BC, SA) = (AD, SA) = $\widehat{SAD}$.

Do tam giác SAD đều nên $\widehat{SAD}$ = 60^o .

Vậy góc giữa hai đường thẳng BC và SA bằng 60°.

Vì ABCD là hình bình hành nên BC // AD. Do đó (BC, SM) = (AD, SM).

Vì M là trung điểm của AD nên SM là đường trung tuyến.

Xét tam giác đều SAD có SM là đường trung tuyến nên SM là đường cao.

Do đó SM $\perp$ AD hay (AD, SM) = 90°.

Vậy góc giữa hai đường thẳng BC và SM bằng 90°.

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: