Cho hình chóp S.ABCD có đáy là hình vuông tâm O và tất cả các cạnh của hình chóp đều bằng a

Bài 7.4 trang 26 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông tâm O và tất cả các cạnh của hình chóp đều bằng a. Gọi M, N lần lượt là trung điểm của cạnh SA, AB.

a) Tính góc giữa các cặp đường thẳng sau: MN và SD; MO và SB.

b) Tính tang của góc giữa hai đường thẳng SN và BC.

Trả lời

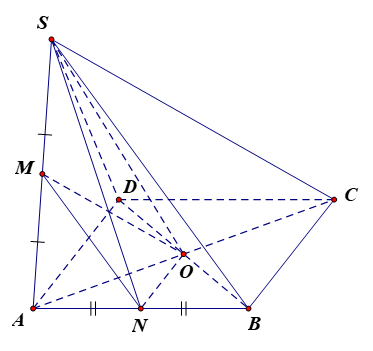
a) Hình chóp S.ABCD có tất cả các cạnh bằng a và đáy ABCD là hình vuông nên

SA = SB = SC = SD = AB = BC = CD = DA = a.

Xét tam giác ADB vuông tại A, có BD² = AD² + AB² = a² + a² = 2a².

Mà SB² + SD² = a² + a² = 2a². Do đó SB² + SD² = BD² nên tam giác SBD vuông tại S.

Vì M, N lần lượt là trung điểm của cạnh SA, AB nên MN là đường trung bình của tam giác SAB, do đó MN // SB.

Khi đó (MN, SD) = (SB, SD) = 90°.

Vì O là giao điểm của AC và BD, ABCD là hình vuông nên O là trung điểm AC, BD.

Xét tam giác SAC có M là trung điểm SA, O là trung điểm AC nên MO là đường trung bình, suy ra MO // SC.

Khi đó (MO, SB) = (SC, SB) = $\widehat{BSC}$ = 60^o (do tam giác SBC là tam giác đều).

b) Xét tam giác ABC có O là trung điểm AC, N là trung điểm AB nên ON là đường trung bình, suy ra ON // BC.

Vì ON // BC nên (SN, BC) = (SN, ON) = $\widehat{SNO}$ .

Vì tam giác SAC có SA = SC = a nên tam giác SAC cân tại S mà SO là trung tuyến nên SO là đường cao.

Vì BD² = 2a² và ABCD là hình vuông nên AC = BD = a$\sqrt{2}$ $\Rightarrow$ AO = OC = $\frac{a\sqrt{2}}{2}$ .

Xét tam giác SOC vuông tại O, có:

SC² = SO² + OC² $\iff$a² = SO² + ${\left(\frac{a\sqrt{2}}{2}\right)}^2\iff$SO = $\frac{a\sqrt{2}}{2}$.

Vì ON là đường trung bình của tam giác ABC nên ON = $\frac{BC}{2}=\frac{a}{2}$.

Xét tam giác đều SAB có SN là trung tuyến đồng thời là đường cao hay SN $\perp$ AB.

Xét tam giác vuông SNB vuông tại N, ta có:

SN² + NB² = SB² $\iff$ SN² + ${\left(\frac{a}{2}\right)}^2$ = a² $\iff$ SN² = $\frac{3a^2}{4}$

Lại có SO² + ON² = ${\left(\frac{a\sqrt{2}}{2}\right)}^2$+ ${\left(\frac{a}{2}\right)}^2$ = $\frac{3a^2}{4}$ . Do đó tam giác SON vuông tại O.

Xét tam giác vuông SON vuông tại O có tan$\widehat{SNO}$ = $\frac{SO}{ON}$ = $\sqrt{2}$.

Vậy tang của góc giữa hai đường thẳng SN và BC là $\sqrt{2}$ .

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác: