Giải SBT Toán 11 (Chân trời sáng tạo) Bài 4: Hàm số lượng giác và đồ thị

Sách bài tập Toán 11 Bài 4: Hàm số lượng giác và đồ thị

Bài 1 trang 26 SBT Toán 11 Tập 1: Tìm tập xác định của các hàm số sau:

a) $y=-\frac{2}{\sin 3x};$

b) $y=\tan \left(\frac{x}{2}-\frac{\pi }{6}\right);$

c) $y=\cot \left(2x-\frac{\pi }{4}\right);$

d) $y=\frac{1}{3-{\cos }^{2}x}.$

Lời giải:

a) $y=-\frac{2}{\text{sin}3x}$ xác định khi sin3x ≠ 0, tức là 3x ≠ kπ, k ∈ ℤ hay $x\ne k\frac{\pi }{3},k\in \mathbb{Z}$

Vậy tập xác định của hàm số là $ℝ\setminus \left\{k\frac{\pi }{3}\mid k\in \mathbb{Z}\right\}$

b) $y=\text{tan}\left(\frac{x}{2}-\frac{\pi }{6}\right)$ xác định khi $\frac{x}{2}-\frac{\pi }{6}\ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$, hay $x\ne \frac{4\pi }{3}+k2\pi ,k\in \mathbb{Z}$.

Vậy tập xác định của hàm số là $ℝ\setminus \left\{\frac{4\pi }{3}+k2\pi \mid k\in \mathbb{Z}\right\}$.

c) $y=\text{cot}\left(2x-\frac{\pi }{4}\right)$ xác định khi $2x-\frac{\pi }{4}\ne k\pi ,k\in \mathbb{Z}$ hay $x\ne \frac{\pi }{8}+k\frac{\pi }{2},k\in \mathbb{Z}$.

Vậy tập xác định của hàm số là $ℝ\setminus \left\{\frac{\pi }{8}+k\frac{\pi }{2}\mid k\in \mathbb{Z}\right\}$.

d) Vì ‒1 ≤ cosx ≤ 1 nên cos²x ≤ 1 với mọi x ∈ ℝ. Suy ra cos² ≠ 3 với mọi x ∈ ℝ.

Do đó hàm số $y=\frac{1}{3-{\text{cos}}^{2}x}$ xác định với mọi x ∈ ℝ.

Vậy tập xác định của hàm số là ℝ.

Bài 2 trang 26 SBT Toán 11 Tập 1: Xét tính chẵn, lẻ của các hàm số sau:

a) $y=\frac{\sin 3x}{x};$

b) $y=-5x^2+c\text{os}\frac{x}{2};$

c) $y=x\sqrt{1+\cos 2x};$

d) $y=\cot x-\frac{2}{\mathrm{s}\text{inx}};$

e) $y=\left|x\right|+\tan x;$

f) $y=\tan \left(x+\frac{\pi }{4}\right).$

Lời giải:

a) Tập xác định của hàm số $y=\frac{\text{sin}3x}{x}$ là $D=ℝ\setminus \left(0\right)$ thoả mãn điều kiện ‒x ∈ D với mọi x ∈ D.

Ta có $\frac{\text{sin}\left(3\left(-x\right)\right)}{-x}=\frac{\text{sin}\left(-3x\right)}{-x}=\frac{-\text{sin}3x}{-x}=\frac{\text{sin}3x}{x}.$

Vậy hàm số $y=\frac{\text{sin}3x}{x}$ là hàm số chẵn.

b) Tập xác định của hàm số $y=-5x^2+\text{cos}\frac{x}{2}$ là D = ℝ thoả mãn điều kiện ‒x ∈ D với mọi x ∈ D.

Ta có $-5{(-x)}^2+\text{cos}\left(\frac{-x}{2}\right)=-5x^2+\text{cos}\frac{x}{2}.$

Vậy hàm số $y=-5x^2+\text{cos}\frac{x}{2}$ là hàm số chẵn.

c) Tập xác định của hàm số $y=x\sqrt{1+\text{cos}2x}$ là D = ℝ thoả mãn điều kiện ‒x ∈ D với mọi x ∈ D.

Ta có $\left(-x\right)\sqrt{1+\text{cos}\left(-2x\right)}=-x\sqrt{1+\text{cos}2x}.$

Vậy hàm số $y=x\sqrt{1+\text{cos}2x}$ là hàm số lẻ.

d) Tập xác định của hàm số $y=\text{cot}x-\frac{2}{\text{sin}x}$ là $D=ℝ\setminus \left(k\pi \mid k\in \mathbb{Z}\right)$ thoả mãn điều kiện ‒x ∈ D với mọi x ∈ D.

Ta có $\text{cot}\left(-x\right)-\frac{2}{\text{sin}\left(-x\right)}=-\text{cot}x+\frac{2}{\text{sin}x}=-\left(\text{cot}x-\frac{2}{\text{sin}x}\right)$.

Vậy hàm số $y=\text{cot}x-\frac{2}{\text{sin}x}$ là hàm số lẻ.

e) Tập xác định của hàm số $y=\left(x\right)+\text{tan}x$ là $D=ℝ\setminus \left(\frac{\pi }{2}+k\pi \mid k\in \mathbb{Z}\right)$ thoả mãn điều kiện ‒x ∈ D với mọi x ∈ D.

Đặt $f\left(x\right)=\left(x\right)+\text{tan}x$. Xét hai giá trị $\frac{\pi }{4}$ và -$\frac{\pi }{4}$ thuộc D, ta có:

$$\begin{gathered} f\left(\frac{\pi }{4}\right)=\left(\frac{\pi }{4}\right)+\text{tan}\frac{\pi }{4}=\frac{\pi }{4}+1 \\ \text{và }f\left(-\frac{\pi }{4}\right)=\left(-\frac{\pi }{4}\right)+\text{tan}\left(-\frac{\pi }{4}\right)=\frac{\pi }{4}-1. \end{gathered}$$

Do $f\left(-\frac{\pi }{4}\right)\ne f\left(\frac{\pi }{4}\right)$ và $f\left(-\frac{\pi }{4}\right)\ne -f\left(\frac{\pi }{4}\right)$ nên $y=\left(x\right)+\text{tan}x$ không là hàm số chẵn cũng không là hàm số lẻ.

g) Tập xác định của hàm số $y=\text{tan}\left(x+\frac{\pi }{4}\right)$ là $D=ℝ\setminus \left(\frac{\pi }{4}+k\pi \mid k\in \mathbb{Z}\right)$ không thoả mãn điều kiện ‒x ∈ D với mọi x ∈ D vì $-\frac{\pi }{4}\in D$ mà $\frac{\pi }{4}\notin D$.

Vậy hàm số $y=\text{tan}\left(x+\frac{\pi }{4}\right)$ không là hàm số chẵn cũng không là hàm số lẻ.

Bài 3 trang 26 SBT Toán 11 Tập 1: Tìm tập giá trị của các hàm số sau:

a) $y=5-2\cos \left(\frac{\pi }{3}-x\right);$

b) $y=\left(\sin 3x\right)-1;$

c) y = 2tanx + 3;

d) $y=\sqrt{1-s\text{inx}}+2.$

Lời giải:

a) $y=5-2\cos \left(\frac{\pi }{3}-x\right)$

TXĐ: D = ℝ.

Ta có $-1\le \cos \left(\frac{\pi }{3}-x\right)\le 1$

$\iff 2\ge -2\cos \left(\frac{\pi }{3}-x\right)\ge -2$

$\iff 7\ge 5-2\cos \left(\frac{\pi }{3}-x\right)\ge 3$

Vậy tập giá trị của hàm số là [3; 7].

b) $y=\left(\sin 3x\right)-1;$

TXĐ: D = ℝ.

Ta có: $0\le \left(\sin 3x\right)\le 1$

$\Rightarrow -1\le \left(\sin 3x\right)-1\le 0$

Vậy tập giá trị của hàm số là [−1; 0].

c) y = 2tanx + 3

TXĐ: D = ℝ.

Ta có tập giá trị của tanx là ℝ nên tập giá trị của hàm số cũng là ℝ.

d) $y=\sqrt{1-s\text{inx}}+2$

Ta có $-1\le \sin x\le 1$ nên $2\ge 1-\sin x\ge 0$ nên hàm số xác định trên ℝ

Khi đó $0\le \sqrt{1-s\text{inx}}\le \sqrt{2}$

Suy ra $2\le \sqrt{1-s\text{inx}}+2\le \sqrt{2}+2$

Vậy tập giá trị của hàm số là $\left(2;2+\sqrt{2}\right)$ .

Bài 4 trang 27 SBT Toán 11 Tập 1: Cho hàm số y = sinx với x ∈ [‒2π; 2π]

a) Vẽ đồ thị hàm số đã cho.

b) Tìm các giá trị của $x\in \left(-\frac{5\pi }{3};\frac{7\pi }{3}\right)$ sao cho $\sin \left(\frac{\pi }{3}-x\right)=-1.$

c) Tìm các giá trị của $x\in \left(-\frac{9\pi }{8};\frac{7\pi }{8}\right)$ sao cho $\sin \left(2x+\frac{\pi }{4}\right)>0.$

d) Tìm m để có 4 giá trị α ∈ [‒2π; 2π] phân biệt thỏa mãn sinα = m.

Lời giải:

a) Ta có đồ thị của hàm số y = sinx trên đoạn [‒2π; 2π] như sau:

b) Đặt $t=\frac{\pi }{3}-x$. Vì $\frac{-5\pi }{3}\le x\le \frac{7\pi }{3}$ nên ‒2π ≤ t ≤ 2π.

Từ đồ thị của hàm số ở trên, ta có:

sint = ‒1 khi và chỉ khi $t=-\frac{\pi }{2}$ hoặc $t=\frac{3\pi }{2}$. Do đó $x=\frac{5\pi }{6}$ hoặc $x=-\frac{7\pi }{6}$.

c) Đặt $t=2x+\frac{\pi }{4}$. Vì $\frac{-9\pi }{8}\le x\le \frac{7\pi }{8}$ nên ‒2π ≤ t ≤ 2π.

Từ đồ thị của hàm số ở trên, ta có:

sint > 0 khi và chỉ khi ‒2π < t < ‒π hoặc 0 < t < π.

Do đó $-\frac{9\pi }{8}<x<-\frac{5\pi }{8}$ hoặc $-\frac{\pi }{8}<x<\frac{3\pi }{8}$.

d) Có bốn giá trị α∈ [‒2π; 2π] thoả mãn sinα = m khi và chỉ khi đường thẳng y = m cắt đồ thị hàm số y = sinα tại bốn điểm. Từ đồ thị hàm số ở trên, ta thấy điều này xảy ra khi và chỉ khi ‒1 < m < 0 hoặc 0 < m < 1.

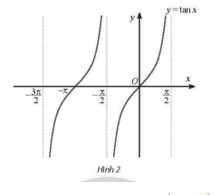
Bài 5 trang 27 SBT Toán 11 Tập 1: Cho hàm số y = tanx với $x\in \left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)\cup \left(-\frac{\pi }{2};\frac{\pi }{2}\right).$

a) Vẽ đồ thị hàm số đã cho.

b) Tìm các giá trị của $x\in \left(-\frac{7\pi }{4};\frac{\pi }{4}\right)$ sao cho $\sqrt{3}\tan \left(x+\frac{\pi }{4}\right)+1=0.$

c) Tìm các giá trị của $x\in \left(-\frac{5\pi }{6};\frac{\pi }{6}\right)$ sao cho $\tan \left(2x+\frac{\pi }{6}\right)\ge -\frac{\sqrt{3}}{3}.$

Lời giải:

a) Ta có đồ thị của hàm số $y=\text{tan}x$ với $x\in \left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)\cup \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ như sau:

b) Ta có $\sqrt{3}\text{tan}\left(x+\frac{\pi }{4}\right)+1=0$ khi và chỉ khi $\text{tan}\left(x+\frac{\pi }{4}\right)=-\frac{\sqrt{3}}{3}$.

Đặt $t=x+\frac{\pi }{4}$. Vì $-\frac{7\pi }{4}\le x\le \frac{\pi }{4}$ nên $-\frac{3\pi }{2}\le t\le \frac{\pi }{2}$, hay $t\in \left(-\frac{3\pi }{2};\frac{\pi }{2}\right)$.

Hàm số y = tant xác định khi $t\ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$. Kết hợp với điều kiện

$t\in \left(-\frac{3\pi }{2};\frac{\pi }{2}\right)$, suy ra $t\in \left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)\phi \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$.

Đồ thị hàm số y = tant với $t\in \left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)\cup \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ như sau:

Từ đồ thị hàm số trên, ta có:

$\text{tan}t=-\frac{\sqrt{3}}{3}$ khi và chỉ khi $t=-\frac{7\pi }{6}$ hoặc $t=-\frac{\pi }{6}$.

Do đó $x=-\frac{17\pi }{12}$ hoặc $x=-\frac{5\pi }{12}$.

c) Đặt $t=2x+\frac{\pi }{6}$. Vì $-\frac{5\pi }{6}\le x\le \frac{\pi }{6}$ nên $-\frac{3\pi }{2}\le t\le \frac{\pi }{2}$, hay $t\in \left(-\frac{3\pi }{2};\frac{\pi }{2}\right)$.

Tương tự câu , từ đồ thị hàm số trên, ta có:

$\text{tan}t\ge -\frac{\sqrt{3}}{3}$ khi và chỉ khi $-\frac{7\pi }{6}\le t<-\frac{\pi }{2}$ hoặc $-\frac{\pi }{6}\le t<\frac{\pi }{2}$.

Do đó $-\frac{2\pi }{3}\le x<-\frac{\pi }{3}$ hoặc $-\frac{\pi }{6}\le x<\frac{\pi }{6}$.

Bài 6 trang 27 SBT Toán 11 Tập 1: Chứng minh rằng các hàm số dưới đây là hàm số tuần hoàn.

a) $y=s\text{inx}-3\tan \frac{x}{2};$

b) y = (cos2x ‒ 1)sinx.

Lời giải:

a) Tập xác định của hàm số là $D=ℝ\setminus \left(\pi +k2\pi \mid k\in \mathbb{Z}\right)$.

Với mọi x ∈ D, ta có:

$$\begin{gathered} x\pm 2\pi \in D \\ \text{và sin}\left(x+2\pi \right)-3\text{tan}\frac{x+2\pi }{2} \\ =\text{sin}x-3\text{tan}\left(\frac{x}{2}+\pi \right)=\text{sin}x-3\text{tan}\frac{x}{2}\text{.} \end{gathered}$$

Do đó hàm số $y=\text{sin}x-3\text{tan}\frac{x}{2}$ là hàm số tuần hoàn.

b) Hàm số $y=\left(\text{cos}2x-1\right)\text{sin}x$ có tập xác định làℝ.

Với mọi x ∈ ℝ, ta có: x ± 2π ∈ ℝ;

$$\begin{gathered} \left(\text{cos}2\left(x+2\pi \right)-1\right)\text{sin}\left(x+2\pi \right) \\ =\left(\text{cos}\left(2x+4\pi \right)-1\right)\text{sin}x \\ =\left(\text{cos}2x-1\right)\text{sin}x\text{.} \end{gathered}$$

Do đó hàm số y = (cos2x ‒ 1)sinx là hàm số tuần hoàn.

Bài 7 trang 27 SBT Toán 11 Tập 1: Huyết áp là áp lực máu cần thiết tác động lên thành động mạch nhằm đưa máu đi nuôi dưỡng các mô trong cơ thế. Nhờ lực co bóp của tim và sức cản của động mạch mà huyết áp được tạo ra. Giả sử huyết áp của một người thay đổi theo thời gian được cho bởi công thức: p(t) = 120 + 15cos150πt, trong đó p(t) là huyết áp tính theo đơn vị mmHg (milimets thủy ngân) và thời gian t tính theo đơn vị phút.

a) Chứng minh p(t) là một phần hàm số tuần hoàn.

b) Huyết áp cao nhất và huyết áp thấp nhất lần lượt được gọi là huyết áp tâm thu và huyết áp tâm trương. Tìm chỉ số huyết áp của người đó, biết rằng chỉ số huyết áp được viết là huyết áp tâm thu/huyết áp tâm trương.

Lời giải:

a) Hàm số p(t) có tập xác định làℝ. Với mọi t ∈ ℝ, ta có $t\pm \frac{1}{75}\in ℝ$ và $p\left(t+\frac{1}{75}\right)=120+15\text{cos}\left(150\pi t+2\pi \right)=120+15\text{cos}150\pi t=p\left(t\right)$.

Do đó p(t) là một hàm số tuần hoàn.

b) Vì ‒1 ≤ cos150πt ≤ 1 với mọi t ∈ ℝ nên 105 ≤ p(t) ≤ 135 với mọi t ∈ ℝ.

Vậy chỉ số huyết áp của người đó là 135/105.

Bài 8 trang 27 SBT Toán 11 Tập 1: Một chất điểm dao động điều hòa theo phương trình $s=3\sin \left(\frac{\pi }{2}t\right)$ với s tính bằng cm và t tình bằng giây. Dựa vào đồ thị của hàm số sin, hãy xác định ở các thời điểm t nào trong 4 giây đầu thì $s\le -\frac{3}{2}.$

Lời giải:

Trong 4 giây đầu, ta có 0 ≤ t ≤ 4, suy ra $0\le \frac{\pi }{2}t\le 2\pi$.

Đặt $x=\frac{\pi }{2}t$, khi đó x ∈ [0; 2π]. Đồ thị của hàm số y = sĩn trên đoạn [0; 2π] như sau:

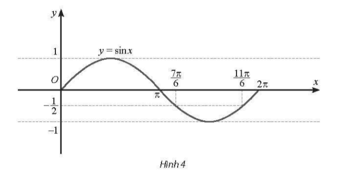
Dựa vào đồ thị trên đoạn [0; 2π], ta có: $s\le -\frac{3}{2}$ khi $3\text{sin}x\le -\frac{3}{2}$ hay $\text{sin}x\le -\frac{1}{2}$

Suy ra $\frac{7\pi }{6}\le x\le \frac{11\pi }{6}$. Do đó $\frac{7}{3}\le t\le \frac{11}{3}$.

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 3: Các công thức lượng giác

Bài 5: Phương trình lượng giác

Bài tập cuối chương 1

Bài 1: Dãy số