Giải SBT Toán 11 Bài 4: Hai mặt phẳng vuông góc
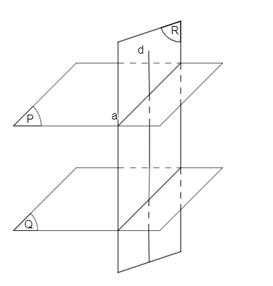
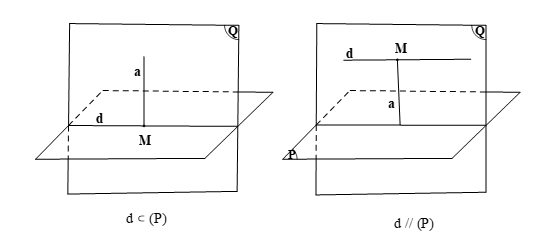
A. Nếu a ⊥ (Q) thì (P) ⊥ (Q);
B. Nếu a ⊥ (Q) thì a ⊥ b với mọi b ⊂ (Q);
C. Nếu a ⊥ (Q) thì (P) // (Q);
D. Nếu a ⊥ (Q) thì a ⊥ d với d = (P) ⋂ (Q).
Lời giải:
Đáp án đúng là: C
· Đáp án A mang nội dung đúng, vì điều kiện để hai mặt phẳng vuông góc với nhau là: nếu mặt phẳng này chứa một đường thẳng mà đường thẳng đó vuông góc với mặt phẳng kia thì hai mặt phẳng đó vuông góc với nhau. Từ đó ta có: a ⊂ (P) nếu a ⊥ (Q) thì (P) ⊥ (Q).
· Đáp án B và D mang nội dung đúng, vì theo định nghĩa của đường thẳng vuông góc với mặt phẳng thì với một đường thẳng vuông góc với mặt phẳng thì đường thẳng đó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
Từ đó ta có: nếu a ⊥ (Q) thì a ⊥ b với mọi b ⊂ (Q);
Và nếu a ⊥ (Q) thì a ⊥ d với d = (P) ⋂ (Q) (vì d ⊂ (Q)).
· Đáp án C mang nội dung sai, vì hai mặt phẳng (P) và (Q) cắt nhau (giả thiết), nên chúng không thể song song với nhau.
A. Nếu a ⊥ d thì a ⊥ (Q);
B. Nếu a ⊥ d thì a // (Q);
C. Nếu a ⊥ d thì a // b với mọi b ⊂ (Q);
C. Nếu a ⊥ d thì a // c với mọi c // (Q).
Lời giải:
Đáp án đúng là: A
· Đáp án A đúng: Lấy mặt phẳng (R) bất kì chứa đường thẳng a và cắt (P) theo giao tuyến là đường thẳng a’.
Ta có: a’ = (R) ∩ (P) và a // (P) nên suy ra a // a’.
Nếu a ⊥ d, mà a // a’ nên a’ ⊥ d.
Lại có: (P) ⊥ (Q), d = (P) ∩ (Q), a’ ⊂ (P) và a’ ⊥ d nên suy ra a’ ⊥ (Q).
Mà a // a’ nên a ⊥ (Q).
Vậy nếu a ⊥ d thì a ⊥ (Q).
· Đáp án B sai: Vì nếu a ⊥ d thì a ⊥ (Q).
· Đáp án C sai: Vì nếu a ⊥ d thì a ⊥ (Q) nên suy ra a ⊥ b với mọi b ⊂ (Q).
· Đáp án D sai:
Lấy mặt phẳng (M) bất kì chứa đường thẳng c và cắt (Q) theo giao tuyến là đường thẳng c’.
Ta có: c’ = (M) ∩ (Q) và c // (Q) nên suy ra c // c’.
Nếu a ⊥ d thì a ⊥ (Q) (cmt), mà c’ ⊂ (Q) nên a ⊥ c’.
Ta thấy: a ⊥ c’, c // c’ nên suy ra a ⊥ c với mọi c // (Q).
Bài 35 trang 103 SBT Toán 11 Tập 2: Hai mặt phẳng cùng vuông góc với mặt phẳng thứ ba thì:
A. Song song với nhau;
B. Trùng nhau;
C. Không song song với nhau;
D. Song song với nhau hoặc cắt nhau theo giao tuyến vuông góc với mặt phẳng thứ ba.
Lời giải:
Đáp án đúng là: D
Giả sử ta có: (P) ⊥ (R), (Q) ⊥ (R), gọi a = (P) ∩ (R), b = (Q) ∩ (R).
Mà (P) và (Q) là hai mặt phẳng phân biệt nên a và b không trùng nhau.
Hơn nữa: a và b cùng nằm trong (R), nên xảy ra hai trường hợp:
· Nếu a // b, mà a ⊂ (P), b ⊂ (Q) nên suy ra (P) // (Q).
· Nếu a cắt b, mà a ⊂ (P) và b ⊂ (Q), nên ta gọi c = (P) ∩ (Q).
Do (P) ⊥ (R), (Q) ⊥ (R) và c = (P) ∩ (Q) nên suy ra c ⊥ (R).
Vậy ta chọn phương án D.
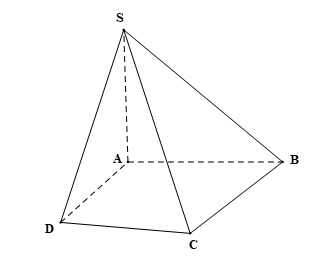
A. SA;
B. SB;
C. SC;
D. SD.
Lời giải:
Đáp án đúng là: A
Vì S ∈ (SAB) ∩ (SAC), A ∈ (SAB) ∩ (SAC) nên suy ra SA = (SAB) ∩ (SAC).
Ta có: (SAB) ⊥ (ABCD), (SAC) ⊥ (ABCD) và SA = (SAB) ∩ (SAC)
Suy ra SA ⊥ (ABCD).
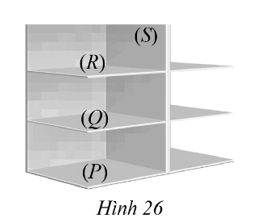
Lời giải:
Dựa vào hình vẽ, ta thấy rằng (P), (Q), (R) là ba mặt phẳng song song với nhau.
Mặt phẳng (S) là mặt thẳng đứng, nên nó vuông góc với cả ba mặt phẳng (P), (Q), (R).
Từ đó ta có thể chỉ ra 2 cặp mặt phẳng vuông góc với nhau là: (P) ⊥ (S), (Q) ⊥ (S).
Bài 38 trang 104 SBT Toán 11 Tập 2: Chứng minh các định lí sau:
a) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai mặt phẳng đó thì vuông góc với mặt phẳng còn lại.
b) Cho một mặt phẳng và một đường thẳng không vuông góc với mặt phẳng đó. Khi đó tồn tại duy nhất một mặt phẳng chứa đường thẳng đã cho và vuông góc với mặt phẳng đã cho.
Lời giải:
a)
Giả sử có ba mặt phẳng (P), (Q), (R) thỏa mãn (P) // (Q) và (R) ⊥ (P). Ta cần chứng minh (R) ⊥ (Q).
Gọi a = (P) ∩ (R), lấy d ⊂ (R) sao cho a ⊥ d.
Ta có: (R) ⊥ (P), a = (R) ∩ (P), d ⊂ (R) và a ⊥ d, suy ra d ⊥ (P).
Mà (P) // (Q), d ⊂ (R) nên d ⊥ (Q).
Suy ra (Q) ⊥ (R).
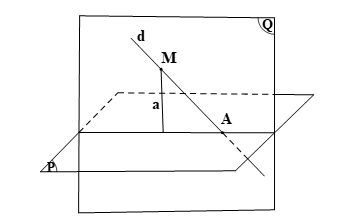
b) Xét đường thẳng d không vuông góc với mặt phẳng (P). Ta cần chứng minh: tồn tại duy nhất mặt phẳng (Q) vuông góc với (P) và chứa d.
Chứng minh tính tồn tại mặt phẳng (Q):
· Xét trường hợp d cắt (P) tại A.
Lấy M ∈ d sao cho M ≠ A. Vẽ đường thẳng a đi qua M sao cho a ⊥ (P).
Suy ra d ∩ a = M.
Khi đó hai đường thẳng a và d xác định mặt phẳng (Q) hay mặt phẳng (Q) chứa hai đường thẳng a và d.
Vì a ⊥ (P), a ⊂ (Q) nên ta có (P) ⊥ (Q).
· Xét trường hợp d ⊂ (P) hoặc d // (P).
Lấy M ∈ d. Vẽ đường thẳng a đi qua M sao cho a ⊥ (P).
Suy ra d ∩ a = M.
Khi đó hai đường thẳng a và d xác định mặt phẳng (Q) hay mặt phẳng (Q) chứa hai đường thẳng a và d.
Vì a ⊥ (P), a ⊂ (Q) nên ta có (P) ⊥ (Q).
Chứng minh tính duy nhất mặt phẳng (Q):
Giả sử tồn tại mặt phẳng (Q’) khác (Q) sao cho d ⊂ (Q’) và (P) ⊥ (Q’).
Ta thấy: d = (Q’) ∩ (Q).
Mà (P) ⊥ (Q), (P) ⊥ (Q’) nên suy ra d ⊥ (P).
Mâu thuẫn với giả thiết d không vuông góc với (P).
Như vậy, tồn tại duy nhất mặt phẳng (Q) sao cho d ⊂ (Q) và (P) ⊥ (Q).
Lời giải:
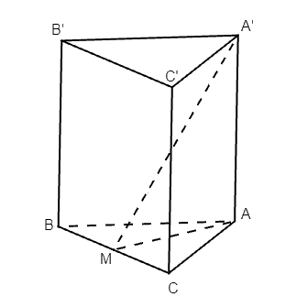
Vì tam giác ABC cân tại A, AM là đường trung tuyến nên AM ⊥ BC.
Ta có: AA’ ⊥ (ABC), AA’ // BB’, suy ra BB’ ⊥ (ABC).
Mà AM ⊂ (ABC) nên BB’ ⊥ AM.
Ta có: AM ⊥ BC, AM ⊥ BB’, BC ∩ BB’ = B trong (BCC’B’).
Từ đó suy ra AM ⊥ (BCC’B’).
Mà AM ⊂ (MAA’) nên (MAA’) ⊥ (BCC’B’).
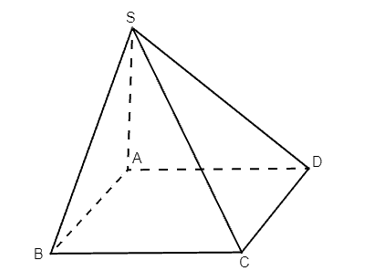
a) (SAB) ⊥ (SBC);
b) (SAD) ⊥ (SCD).
Lời giải:
a) Ta có: SA ⊥ (ABCD), BC ⊂ (ABCD) suy ra SA ⊥ BC.
Vì ABCD là hình chữ nhật nên BC ⊥ AB.
Ta có: BC ⊥ SA, BC ⊥ AB, SA ∩ AB = A trong (SAB)
Suy ra BC ⊥ (SAB).
Hơn nữa BC ⊂ (SBC)
Từ đó ta có: (SAB) ⊥ (SBC).
b) Ta có: SA ⊥ (ABCD), CD ⊂ (ABCD) suy ra SA ⊥ CD.
Vì ABCD là hình chữ nhật nên CD ⊥ AD.
Ta có: CD ⊥ SA, CD ⊥ AD, SA ∩ AD = A trong (SAD)
Suy ra CD ⊥ (SAD).
Hơn nữa CD ⊂ (SCD)
Từ đó ta có: (SAD) ⊥ (SCD).
Lời giải:
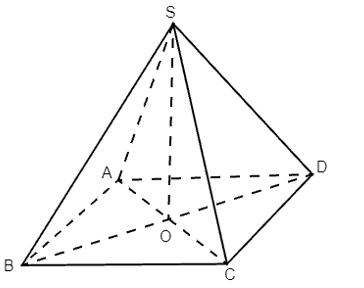
Gọi O là giao điểm của AC và BD.
Suy ra: O ∈ AC ⊂ (SAC) và O ∈ BD ⊂ (SBD) nên O ∈ (SAC) ∩ (SBD).
Hơn nữa S ∈ (SAC) ∩ (SBD).
Nên SO = (SAC) ∩ (SBD).
Vì (SAC) ⊥ (ABCD), (SBD) ⊥ (ABCD) và SO = (SAC) ∩ (SBD), ta suy ra SO ⊥ (ABCD).
Mà AC ⊂ (ABCD) nên SO ⊥ AC.
Do ABCD là hình thoi, nên AC ⊥ BD.
Ta có: AC ⊥ SO, AC ⊥ BD và SO ∩ BD = O trong (SBD).
Suy ra AC ⊥ (SBD).
Mặt khác AC ⊂ (SAC).
Từ đó ta có: (SAC) ⊥ (SBD).
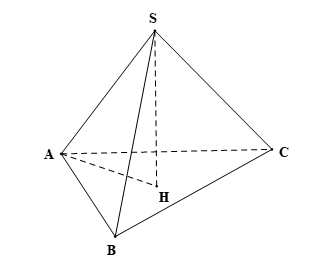
Lời giải:
Do H là trực tâm của tam giác ABC nên AH ⊥ BC.
Do nên ta có: SA ⊥ SB và SA ⊥ SC.
Ta có: SA ⊥ SB, SA ⊥ SC và SB ∩ SC = S trong (SBC)
Suy ra SA ⊥ (SBC).
Mà BC ⊂ (SBC) nên SA ⊥ BC.
Ta có: BC ⊥ AH, BC ⊥ SA và AH ∩ SA = A trong (SAH)
Suy ra BC ⊥ (SAH).
Hơn nữa BC ⊂ (ABC).
Từ đó ta có (SAH) ⊥ (ABC).
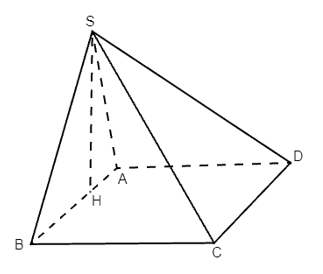
a) (SAD) ⊥ (SAB);
b) (SBC) ⊥ (SAB);
c) (SAD) ⊥ (SBC).
Lời giải:
a) Gọi H là hình chiếu của S trên AB.
Ta có: (SAB) ⊥ (ABCD), (SAB) ∩ (ABCD) = AB và SH ⊂ (SAB), SH ⊥ AB
Suy ra SH ⊥ (ABCD).
Mà AD ⊂ (ABCD) nên SH ⊥ AD.
Do ABCD là hình vuông nên ta có AD ⊥ AB.
Ta có: AD ⊥ SH, AD ⊥ AB và SH ∩ AB = H trong (SAB)
Suy ra AD ⊥ (SAB).
Hơn nữa AD ⊂ (SAD) nên (SAD) ⊥ (SAB).
b) Vì SH ⊥ (ABCD) và BC ⊂ (ABCD) nên SH ⊥ BC.
Do ABCD là hình vuông nên ta có BC ⊥ AB.
Ta có: BC ⊥ SH, BC ⊥ AB và SH ∩ AB = H trong (SAB)
Suy ra BC ⊥ (SAB).
Hơn nữa BC ⊂ (SBC) nên (SBC) ⊥ (SAB).
c) Vì AD ⊥ (SAB) và SB ⊂ (SAB) nên AD ⊥ SB.
Theo giả thiết: tam giác SAB vuông tại S nên ta có SB ⊥ SA.
Ta có: SB ⊥ AD, SB ⊥ SA và AD ∩ SA = A trong (SAD)
Suy ra SB ⊥ (SAD).
Hơn nữa SB ⊂ (SBC) nên (SAD) ⊥ (SBC).
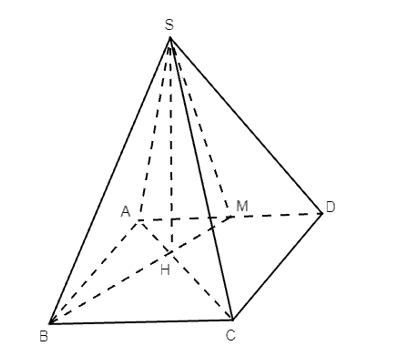
Lời giải:
Gọi H là giao điểm của BM và AC.
Suy ra: H ∈ BM ⊂ (SBM) và H ∈ AC ⊂ (SAC) nên ta có H ∈ (SBM) ∩ (SAC).
Mà S ∈ (SBM) ∩ (SAC).
Từ đó suy ra: SH = (SBM) ∩ (SAC).
Ta có: (SAC) ⊥ (ABCD), (SBM) ⊥ (ABCD), SH = (SBM) ∩ (SAC).
Suy ra SH ⊥ (ABCD), tức H là hình chiếu vuông góc của S trên (ABCD).
Nên góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng góc giữa hai đường thẳng SA và AH và bằng
Do ABCD là hình chữ nhật nên
Áp dụng định lí Pythagore trong tam giác ADC vuông tại D có:
AC2 = AD2 + DC2
(vì DC = AB do ABCD là hình chữ nhật).
Do M là trung điểm của AD nên
Do ABCD là hình chữ nhật nên AD // BC hay AM // BC.
Áp dụng hệ quả định lí Thalès với AM // BC ta có:
Vì SH ⊥ (ABCD) và AH ⊂ (ABCD) nên SH ⊥ AH.
Xét tam giác SAH vuông tại H có:
Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 2: Đường thẳng vuông góc với mặt phẳng
Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối