Trong mặt phẳng toạ độ Oxy cho ba điểm M(4; 0), N(5; 2) và P(2, 3). Tìm toạ độ các đỉnh của tam giác

Bài 4.22 trang 58 SBT Toán 10 Tập 1: Trong mặt phẳng toạ độ Oxy cho ba điểm M(4; 0), N(5; 2) và P(2, 3). Tìm toạ độ các đỉnh của tam giác ABC, biết M, N, P theo thứ tự là trung điểm cạnh BC, CA, AB.

Trả lời

Cách 1:

Gọi A(x_A; y_A); B(x_B; y_B) và C(x_C; y_C) là tọa độ ba đỉnh của tam giác ABC.

Ta có:

+) M(4; 0) là trung điểm của BC nên $\left\{\begin{array}{l}4=\frac{x_B+x_C}{2}\\ 0=\frac{y_B+y_C}{2}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}{x}_B+x_C=8\\ y_B+y_C=0\end{array}\right.$                                 (1)

+) N(5; 2) là trung điểm của CA nên $\left\{\begin{array}{l}5=\frac{x_A+x_C}{2}\\ 2=\frac{y_A+y_C}{2}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}{x}_A+x_C=10\\ y_A+y_C=4\end{array}\right.\iff \left\{\begin{array}{l}{x}_C=10-x_A\\ y_C=4-y_A\end{array}\right.$     (2)

+) P(2; 3) là trung điểm của AB nên $\left\{\begin{array}{l}2=\frac{x_A+x_B}{2}\\ 3=\frac{y_A+y_B}{2}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}{x}_A+x_B=4\\ y_A+y_B=6\end{array}\right.\iff \left\{\begin{array}{l}{x}_B=4-x_A\\ y_B=6-y_A\end{array}\right.$        (3)

Thay (2) và (3) vào (1) ta được:

$\left\{\begin{array}{l}\left(4-x_A\right)+\left(10-x_A\right)=8\\ \left(6-y_A\right)+\left(4-y_A\right)=0\end{array}\right.$$\iff \left\{\begin{array}{l}14-2x_A=8\\ 10-2y_A=0\end{array}\right.$

$\iff \left\{\begin{array}{l}{x}_A=3\\ y_A=5\end{array}\right.$ $\Rightarrow$ A(3; 5)

Khi đó $\left\{\begin{array}{l}{x}_B=4-3=1\\ y_B=6-5=1\end{array}\right.$ $\Rightarrow$ B(1; 1)

$\left\{\begin{array}{l}{x}_C=10-3=7\\ y_C=4-5=-1\end{array}\right.$$\Rightarrow$ C(7; –1)

Vậy A(3; 5), B(1; 1) và C(7; –1).

Cách 2:

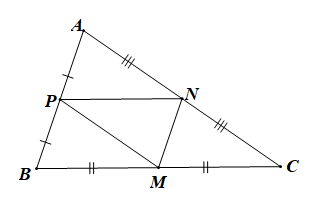
Do M, N, P lần lượt là trung điểm của BC, CA, AB

Nên MN, NP, PM là các đường trung bình của tam giác ABC.

$\Rightarrow$ MN // AB, NP // BC, MP // AC.

+) Do MN // BM và NP // BM nên tứ giác MNPB là hình bình hành

$\Rightarrow \overrightarrow{MB}=\overrightarrow{NP}$

Gọi B(x_B; y_B) và có M(4; 0), N(5; 2) và P(2, 3).

$\Rightarrow \overrightarrow{MB}=\left(x_B-4;y_B\right)$ và $\overrightarrow{NP}=\left(2-5;3-2\right)=\left(-3;1\right)$

Khi đó $\overrightarrow{MB}=\overrightarrow{NP}\iff \left\{\begin{array}{l}{x}_B-4=-3\\ y_B=1\end{array}\right.$$\iff \left\{\begin{array}{l}{x}_B=1\\ y_B=1\end{array}\right.$ Þ B(1; 1)

Tương tự ta cũng có A(3; 5) và C(7; –1).

Vậy A(3; 5), B(1; 1) và C(7; –1).

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vectơ với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số