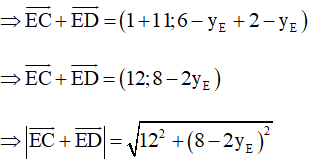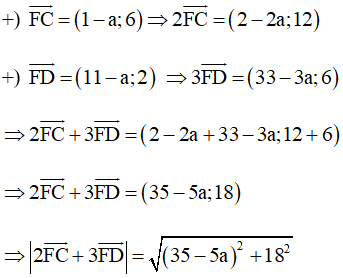Trong mặt phẳng toạ độ Oxy cho hai điểm C(1; 6) và D(11; 2). a) Tìm toạ độ của điểm E
123
11/01/2024
Bài 4.26 trang 60 SBT Toán 10 Tập 1:
Trong mặt phẳng toạ độ Oxy cho hai điểm C(1; 6) và D(11; 2).
a) Tìm toạ độ của điểm E thuộc trục tung sao cho vectơ →EC+→ED có độ dài ngắn nhất.
b) Tìm toạ độ của điểm F thuộc trục hoành sao cho |2→FC+3→FD| đạt giá trị nhỏ nhất.
c) Tìm tập hợp các điểm M sao cho |→MC+→MD|=CD.
Trả lời
a) Giả sử E(0; yE) là điểm thuộc trục tung.
Với C(1; 6) và D(11; 2) ta có:
→EC=(1;6−yE) và →ED=(11;2−yE)
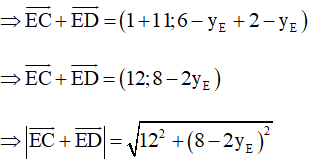
Vì (8 – 2yE)2 ≥ 0 ∀ yE
Nên 122 + (8 – 2yE)2 ≥ 122 ∀ yE
Hay √122+(8−2yE)2≥12 ∀ yE
⇒|→EC+→ED|≥12 ∀ yE
Do đó độ dài của vectơ →EC+→ED nhỏ nhất bằng 12
Dấu “=’ xảy ra ⇒ 8 – 2yE = 0
⇒ yE = 4
Vậy với E(0; 4) thì vectơ →EC+→ED có độ dài ngắn nhất.
b) Giả sử F(a; 0) thuộc trục hoành.
Với C(1; 6) và D(11; 2) ta có:
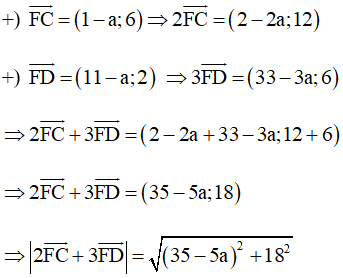
Vì (35 – 5a)2 ≥ 0 ∀a
Nên (35 – 5a)2 + 182 ≥ 182 ∀a
Hay √(35−5a)2+182 ∀a
⇒|2→FC+3→FD|≥18 ∀a
Do đó độ dài của vectơ 2→FC+3→FD nhỏ nhất bằng 18
Dấu “=’ xảy ra ⇒ 35 – 5a = 0
⇒ a = 7
Vậy với F(7; 0) thì |2→FC+3→FD| đạt giá trị nhỏ nhất.
c) Giả sử M(x ; y) là tọa độ điểm thỏa mãn |→MC+→MD|=CD.
Với C(1; 6) và D(11; 2) ta có:
+) →CD=(10;−4)
⇒CD=|→CD|=√102+(−4)2=√116=2√29
Gọi I là trung điểm của CD, khi đó ta có:
• Tọa độ của I là: {xI=1+112=6yI=6+22=4 Þ I(6; 4).
• →MC+→MD=2→MI
⇒|→MC+→MD|=|2→MI|=2.MI
Ta có
|→MC+→MD|=CD⇔2MI=CD
⇔IM=CD2=2√292=√29.
Do đó tập hợp điểm M là đường tròn tâm I(6; 4) và bán kính R=√29.
Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 8: Tổng và hiệu của hai vectơ
Bài 9: Tích của một vectơ với một số
Bài 10: Vectơ trong mặt phẳng tọa độ
Bài 11: Tích vô hướng của hai vectơ
Bài tập cuối chương 4
Bài 12: Số gần đúng và sai số