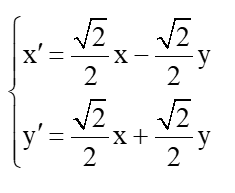Giải Chuyên đề Toán 11 Bài 1 (Chân trời sáng tạo): Phép biến hình và phép dời hình

Giải Chuyên đề Toán 11 Bài 1: Phép biến hình và phép dời hình

Khởi động trang 6 Chuyên đề Toán 11: Bức tranh trang trí trong hình bên trước khi tô màu thực chất được tạo ra từ một hình mũi tên duy nhất và được dời chỗ tới các vị trí khác nhau. Hãy thảo luận để tìm hiểu về các phép biến đổi hình học nào đã tạo ra tất cả các hình mũi tên như vậy từ một hình mũi tên ban đầu.

Lời giải:

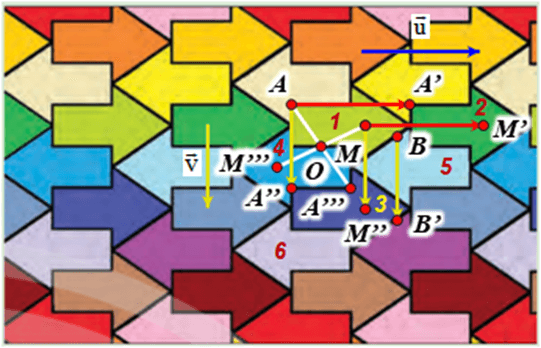
Giả sử mũi tên ban đầu là mũi tên đánh số 1.

⦁ Gọi A là một điểm trên hình mũi tên 1 và $\overrightarrow{u}$ có phương song song với trục đối xứng của hình mũi tên 1, độ dài của $\overrightarrow{u}$ bằng độ dài từ điểm đầu tới điểm cuối của mũi tên 1 (hình vẽ).

Lấy điểm A’ sao cho $\overrightarrow{{\mathrm{AA}}^{\text{'}}}=\overrightarrow{u}$.

Khi đó điểm A’ là một điểm trên hình mũi tên 2 có vị trí tương ứng với điểm A trên hình mũi tên 1.

Tương tự, với mỗi điểm M bất kì trên hình mũi tên 1, ta lấy điểm M’ sao cho $\overrightarrow{{\mathrm{MM}}^{\text{'}}}=\overrightarrow{u}$ thì từ hình mũi tên 1 là tập hợp điểm M, ta được tập hợp các điểm M’ tạo thành hình mũi tên 2.

⦁ Gọi A’’ là một điểm trên hình mũi tên 3 có vị trí tương ứng với điểm A trên hình mũi tên 1.

Giả sử $\overrightarrow{v}$ là vectơ có phương vuông góc với trục đối xứng của hình mũi tên 1, độ dài bằng độ dài từ điểm A đến điểm A’’ (hình vẽ).

Tức là, $\overrightarrow{v}=\overrightarrow{{\mathrm{AA}}^{\text{'}\text{'}}}$ .

Gọi B là một điểm trên hình mũi tên 1.

Lấy điểm B’ sao cho $\overrightarrow{{\mathrm{BB}}^{\text{'}}}=\overrightarrow{v}$ .

Khi đó điểm B’ là một điểm trên hình mũi tên 3 có vị trí tương ứng với điểm B trên hình mũi tên 1.

Tương tự, với mỗi điểm M bất kì trên hình mũi tên 1, ta lấy điểm M’’ sao cho $\overrightarrow{M{M}^{\text{'}\text{'}}}=\overrightarrow{v}$ thì từ hình mũi tên 1 là tập hợp điểm M, ta được tập hợp các điểm M’’ tạo thành hình mũi tên 3.

⦁ Gọi O là một điểm trên hình mũi tên 1 (hình vẽ).

Lấy điểm A’’’ đối xứng với A qua O.

Khi đó điểm A’’’ là một điểm trên hình mũi tên 4 có vị trí tương ứng với điểm A trên hình mũi tên 1.

Tương tự, với mỗi điểm M bất kì trên hình mũi tên 1, ta lấy điểm M’’’ đối xứng với M qua O thì từ hình mũi tên 1 là tập hợp điểm M, ta được tập hợp các điểm M’’’ tạo thành hình mũi tên 4.

⦁ Tương tự trường hợp chứng minh từ hình mũi tên 1 thành hình mũi tên 2, ta chứng minh được trường hợp từ hình mũi tên 4 thành hình mũi tên 5.

⦁ Tương tự trường hợp chứng minh từ hình mũi tên 1 thành hình mũi tên 3, ta chứng minh được trường hợp từ hình mũi tên 4 thành hình mũi tên 6.

• Tương tự như vậy với tất cả các hình mũi tên khác.

Vậy hai phép biến đổi hình học cần tìm là phép biến đổi theo vectơ $\overrightarrow{u}$ có phương song song với trục đối xứng, độ dài bằng độ dài từ điểm đầu tới điểm cuối của mũi tên ban đầu và phép biến đổi lấy điểm đối xứng qua một điểm.

1. Phép biến hình

Khám phá 1 trang 6 Chuyên đề Toán 11: Trong mặt phẳng, cho đường thẳng d và điểm M. Gọi M’ là hình chiếu vuông góc của M trên đường thẳng d.

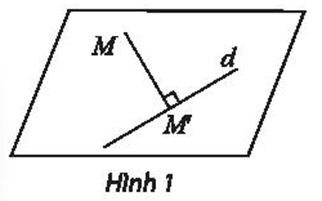
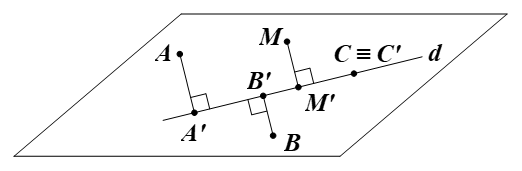
Vẽ ba điểm A, B, C tùy ý và tìm hình chiếu vuông góc A’, B’, C’ của chúng trên d.

Lời giải:

Giả sử chọn ba điểm A, B, C như hình vẽ dưới đây. Khi đó hình chiếu vuông góc A’, B’, C’ của chúng trên d được biểu diễn như hình vẽ dưới đây:

Thực hành 1 trang 7 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, ứng mỗi điểm M(x; y) quy tắc f xác định điểm M’(–3x; 3y). Hãy cho biết f có phải là phép biến hình không. Nếu có, tìm ảnh của điểm A(–1; 2) qua f.

Lời giải:

⦁ Theo đề, ta có f(M) = M’, với tọa độ M(x; y), M’(–3x; 3y).

Ta thấy f là một quy tắc sao cho: ứng với mỗi điểm M đều xác định duy nhất một điểm M’.

Vậy f là một phép biến hình.

⦁ Gọi A’ là ảnh của điểm A(–1; 2) qua phép biến hình f.

Ta có x_A’ = –3x_A = –3.(–1) = 3 và y_A’ = 3y_A = 3.2 = 6.

Vậy ảnh của điểm A(–1; 2) qua phép biến hình f là điểm A’(3; 6).

2. Phép dời hình

Khám phá 2 trang 7 Chuyên đề Toán 11: Khi một ô tô dời chỗ đậu từ vị trí M đến M’, khoảng cách giữa hai trục bánh xe có thay đổi không?

Lời giải:

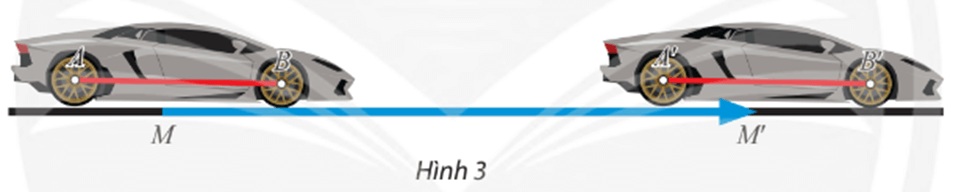
Khi một ô tô dời chỗ đậu từ vị trí M đến M’, khoảng cách giữa hai trục bánh xe không thay đổi.

Thực hành 2 trang 8 Chuyên đề Toán 11: Cho điểm O trong mặt phẳng. Ta định nghĩa một phép biến hình h như sau: Với mỗi điểm M khác O chọn M’ = h(M) sao cho O là trung điểm của đoạn thẳng MM’ (Hình 6), còn với M trùng với O thì ta chọn O = h(M). Chứng minh h là một phép dời hình.

Lời giải:

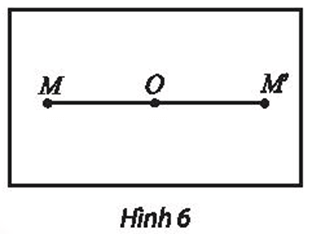
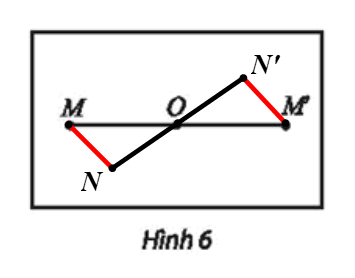
⦁ Với hai điểm M, N khác O, ta đặt M’ = h(M) và N’ = h(N) với O là trung điểm của MM’ và O cũng là trung điểm của NN’.

Suy ra tứ giác MNM’N’ là hình bình hành.

Do đó MN = M’N’ (1)

⦁ Với M trùng O, ta có O = h(M).

Suy ra MO = 0 (2)

Từ (1), (2), ta thu được h là một phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.

Vậy h là một phép dời hình.

Vận dụng trang 8 Chuyên đề Toán 11: Một người đã vẽ xong bức tranh một con thiên nga đang bơi trên mặt hồ (đường thẳng d) (Hình 7a). Người đó muốn vẽ bóng của con thiên nga đó xuống mặt nước (như Hình 7b) bằng cách gấp tờ giấy theo đường thẳng d và đồ theo hình con thiên nga trên nửa tờ giấy còn lại. Chứng tỏ rằng đây là một phép dời hình.

Lời giải:

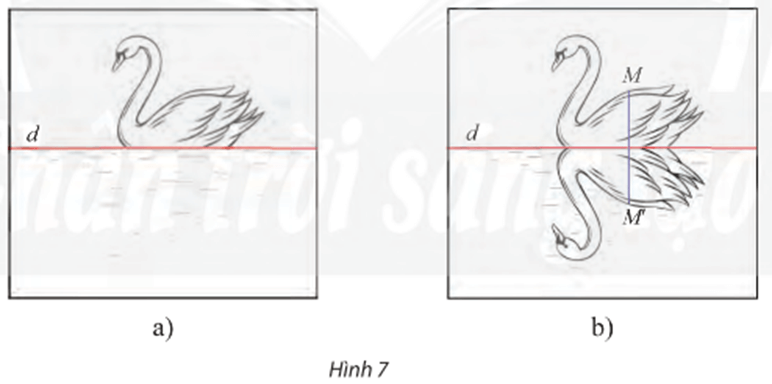
Ta đặt f là phép biến hình biến con thiên nga trong bức tranh thành bóng của con thiên nga đó qua đường thẳng d (mặt hồ).

Chọn M’ = f(M) hay M’ là điểm đối xứng của M qua d.

Suy ra d là đường trung trực của đoạn thẳng MM’.

Gọi H là giao điểm của MM’ và d.

Khi đó H là trung điểm của MM’ và MM’ ⊥ d tại H.

Trên hình 7b, chọn điểm N tùy ý trên con thiên nga đã vẽ trên mặt hồ (như hình vẽ).

Chọn N’ = f(N) hay N’ là điểm đối xứng của N qua d.

Suy ra d là đường trung trực của đoạn thẳng NN’.

Gọi K là giao điểm của NN’ và d.

Khi đó K là trung điểm của NN’ và NN’ ⊥ d tại K.

Ta có $\overrightarrow{\mathrm{MN}}+\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}=\left(\overrightarrow{\mathrm{MH}}+\overrightarrow{\mathrm{HK}}+\overrightarrow{\mathrm{KN}}\right)+\left(\overrightarrow{{\mathrm{M}}^{\text{'}}\mathrm{H}}+\overrightarrow{\mathrm{HK}}+\overrightarrow{{\mathrm{KN}}^{\text{'}}}\right)$

$=\left(\overrightarrow{\mathrm{MH}}+\overrightarrow{{\mathrm{M}}^{\text{'}}\mathrm{H}}\right)+\left(\overrightarrow{\mathrm{KN}}+\overrightarrow{{\mathrm{KN}}^{\text{'}}}\right)+2\overrightarrow{\mathrm{HK}}$

$=\overrightarrow{0}+\overrightarrow{0}+2\overrightarrow{\mathrm{HK}}$ (do H, K lần lượt là trung điểm của MM’, NN’)

$=2\overrightarrow{\mathrm{HK}}$

Lại có $\overrightarrow{\mathrm{MN}}-\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}=\left(\overrightarrow{\mathrm{HN}}-\overrightarrow{\mathrm{HM}}\right)-\left(\overrightarrow{{\mathrm{HN}}^{\text{'}}}-\overrightarrow{{\mathrm{HM}}^{\text{'}}}\right)$

$=\overrightarrow{\mathrm{HN}}-\overrightarrow{\mathrm{HM}}-\overrightarrow{{\mathrm{HN}}^{\text{'}}}+\overrightarrow{{\mathrm{HM}}^{\text{'}}}$

$=\left(\overrightarrow{\mathrm{HN}}-\overrightarrow{{\mathrm{HN}}^{\text{'}}}\right)+\left(\overrightarrow{{\mathrm{HM}}^{\text{'}}}-\overrightarrow{\mathrm{HM}}\right)=\overrightarrow{{\mathrm{N}}^{\text{'}}\mathrm{N}}+\overrightarrow{{\mathrm{MM}}^{\text{'}}}$

Ta có ${\overrightarrow{\mathrm{MN}}}^2-{\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}}^2=\left(\overrightarrow{\mathrm{MN}}+\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}\right)\left(\overrightarrow{\mathrm{MN}}-\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}\right)=2\overrightarrow{\mathrm{HK}}\left(\overrightarrow{{\mathrm{N}}^{\text{'}}\mathrm{N}}+\overrightarrow{{\mathrm{MM}}^{\text{'}}}\right)$

$=2\overrightarrow{\mathrm{HK}}.\overrightarrow{{\mathrm{N}}^{\text{'}}\mathrm{N}}+2\overrightarrow{\mathrm{HK}}.\overrightarrow{{\mathrm{MM}}^{\text{'}}}=2.0+2.0=0$ (do MM’ ⊥ d và NN’ ⊥ d).

Suy ra ${\overrightarrow{\mathrm{MN}}}^2={\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}}^2$

Do đó MN = M’N’.

Vì vậy phép biến hình f bảo toàn khoảng cách giữa hai điểm bất kì.

Vậy ta có điều phải chứng minh.

3. Tính chất của phép dời hình

Khám phá 3 trang 8 Chuyên đề Toán 11: Trong mỗi trường hợp dưới đây, cho f là một phép dời hình.

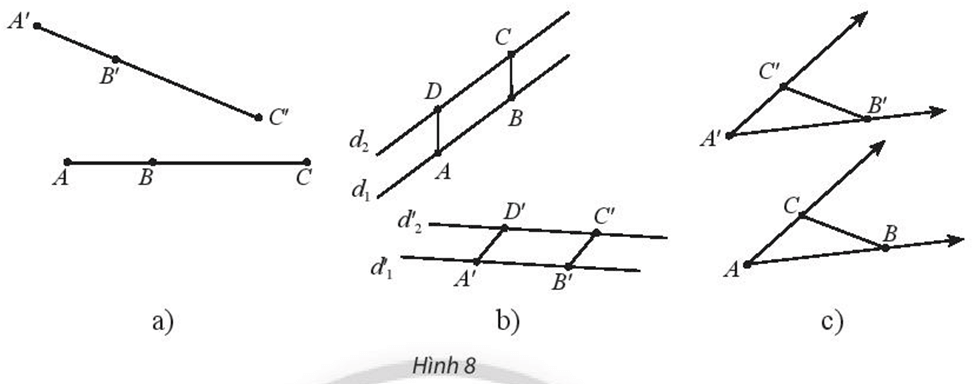
a) Cho ba điểm A, B, C thẳng hàng theo thứ tự (B nằm giữa A và C). Gọi A’, B’, C’ lần lượt là ảnh của A, B, C qua f (Hình 8a). Có nhận xét gì về vị trí tương đối của ba điểm A’, B’, C’?

b) Cho hai đường thẳng song song d₁ và d₂, lấy hai đoạn thẳng bằng nhau AB và DC lần lượt trên d₁ và d₂. Gọi ${d^{\text{'}}}_1,{d^{\text{'}}}_2$ lần lượt là ảnh của d₁, d₂ và A’, B’, C’, D’ lần lượt là ảnh của A, B, C, D qua f (Hình 8b). Tứ giác A’B’C’D’ là hình gì? Nêu nhận xét về vị trí tương đối của hai đường thẳng ${d^{\text{'}}}_1,{d^{\text{'}}}_2$ .

c) Cho A’B’C’ là ảnh của tam giác ABC qua f (Hình 8c).

So sánh ∆A’B’C’ và ∆ABC. So sánh số đo hai góc $\widehat{\mathrm{BAC}}$ và $\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}$ .

Lời giải:

Phép dời hình f bảo toàn khoảng cách giữa hai điểm bất kì.

a) Ta có A’, B’, C’ lần lượt là ảnh của A, B, C qua phép dời hình f.

Suy ra A’B’ = AB; B’C’ = BC và A’C’ = AC.

Theo đề, ta có ba điểm A, B, C thẳng hàng theo thứ tự (B nằm giữa A và C).

Suy ra AB + BC = AC.

Khi đó A’B’ + B’C’ = A’C’.

Vậy ba điểm A’, B’, C’ thẳng hàng theo thứ tự (B’ nằm giữa A’ và C’).

b) Ta có AB = DC (giả thiết) và AB // DC (do d₁ // d₂).

Suy ra tứ giác ABCD là hình bình hành.

Khi đó AD = BC.

Ta có A’, B’, C’, D’ lần lượt là ảnh của A, B, C, D qua phép dời hình f.

Suy ra A’B’ = AB; D’C’ = DC.

Mà AB = DC (giả thiết), do đó A’B’ = D’C’ (1)

Chứng minh tương tự, ta được A’D’ = B’C’ (2)

Từ (1), (2), suy ra tứ giác A’B’C’D’ là hình bình hành.

Khi đó A’B’ // D’C’ hay ${d^{\text{'}}}_1\text{//}{d^{\text{'}}}_2$ .

Vậy tứ giác A’B’C’D’ là hình bình hành và ${d^{\text{'}}}_1\text{//}{d^{\text{'}}}_2$.

c) Ta có tam giác A’B’C’ là ảnh của tam giác ABC qua phép dời hình f.

Suy ra A’, B’, C’ lần lượt là ảnh của A, B, C qua phép dời hình f.

Vì vậy A’B’ = AB; B’C’ = BC và A’C’ = AC.

Do đó ∆A’B’C’ = ∆ABC (c.c.c).

Từ đó suy ra $\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}=\widehat{\mathrm{BAC}}$ (cặp cạnh tương ứng).

Vậy ∆A’B’C’ = ∆ABC và $\widehat{B^{\text{'}}{A}^{\text{'}}{C}^{\text{'}}}=\widehat{\mathrm{BAC}}$ .

Thực hành 3 trang 10 Chuyên đề Toán 11: Gọi A’B’C’D’ là ảnh của hình chữ nhật ABCD qua phép biến hình được diễn tả trong Vận dụng. Hãy cho biết A’B’C’D’ là hình gì. Giải thích.

Lời giải:

Gọi f là phép biến hình trong Vận dụng.

Trong Vận dụng, ta đã chứng minh được f là một phép dời hình.

Ta có ABCD là hình chữ nhật.

Suy ra $\widehat{\mathrm{DAB}}=90°;\widehat{\mathrm{ABC}}=90°;\widehat{\mathrm{BCD}}=90°$

Do phép dời hình f bảo toàn độ lớn của góc nên ta có $\widehat{{\mathrm{D}}^{\text{'}}{\mathrm{A}}^{\text{'}}{\mathrm{B}}^{\text{'}}}=90°;$ $\widehat{{\mathrm{A}}^{\text{'}}{\mathrm{B}}^{\text{'}}{\mathrm{C}}^{\text{'}}}=90°;$ $\widehat{{\mathrm{B}}^{\text{'}}{\mathrm{C}}^{\text{'}}{\mathrm{D}}^{\text{'}}}=90°$

Vậy A’B’C’D’ cũng là hình chữ nhật.

Bài tập

Bài 1 trang 10 Chuyên đề Toán 11: Cho đường thẳng d đi qua tâm O của đường tròn (C) và cắt (C) tại A và B. Tìm ảnh của đường tròn (C) qua phép chiếu vuông góc lên d.

Lời giải:

Ta đặt f là phép chiếu vuông góc lên d.

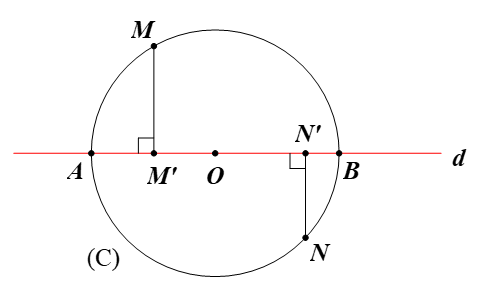
Vì A, B là giao điểm của đường thẳng d và đường tròn (C) nên A = f(A), B = f(B) (1)

Lấy điểm M ∈ (C) sao cho M ≠ A và M ≠ B.

Kẻ MM’ ⊥ d tại M’.

Khi đó ta có M’ = f(M).

Mà AB là đường kính của đường tròn (C) nên M’ nằm trên đoạn thẳng AB.

Tương tự như vậy, mỗi điểm N bất kì di động trên đường tròn (C) sao cho N ≠ A và N ≠ B thì ảnh N’ của N qua f đều nằm trên đoạn thẳng AB (2)

Từ (1), (2), ta thu được ảnh của đường tròn (C) qua phép chiếu vuông góc lên d là đoạn thẳng AB hay f((C)) = AB.

Bài 2 trang 10 Chuyên đề Toán 11: Cho đường thẳng d cố định, xét phép biến hình f biến điểm M thuộc d thành chính nó và biến điểm M không thuộc d thành điểm M’ sao cho d là trung trực của đoạn MM’. Hãy chứng minh f là một phép dời hình.

Lời giải:

• Phép biến hình f biến 1 điểm thuộc d thành chính nó, do đó khoảng cách giữa hai điểm bất kì thuộc d qua phép biến hình f được bảo toàn (1)

• Lấy hai điểm M, N bất kì không thuộc d.

Ta có M’ = f(M) và N’ = f(N).

Gọi H, K lần lượt là trung điểm của MM’ và NN’.

Suy ra $\overrightarrow{\mathrm{MH}}+\overrightarrow{{\mathrm{M}}^{\text{'}}\mathrm{H}}=\overrightarrow{0};\overrightarrow{\mathrm{KN}}+\overrightarrow{{\mathrm{KN}}^{\text{'}}}=\overrightarrow{0}$

Ta có:

⦁ $\overrightarrow{\mathrm{MN}}+\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}=\left(\overrightarrow{\mathrm{MH}}+\overrightarrow{\mathrm{HK}}+\overrightarrow{\mathrm{KN}}\right)+\left(\overrightarrow{{\mathrm{M}}^{\text{'}}\mathrm{H}}+\overrightarrow{\mathrm{HK}}+\overrightarrow{{\mathrm{KN}}^{\text{'}}}\right)$

$=\left(\overrightarrow{\mathrm{MH}}+\overrightarrow{{\mathrm{M}}^{\text{'}}\mathrm{H}}\right)+\left(\overrightarrow{\mathrm{KN}}+\overrightarrow{{\mathrm{KN}}^{\text{'}}}\right)+2\overrightarrow{\mathrm{HK}}$

$=\overrightarrow{0}+\overrightarrow{0}+2\overrightarrow{\mathrm{HK}}$ (do H, K lần lượt là trung điểm của MM’, NN’)

$=2\overrightarrow{\mathrm{HK}}$

⦁ $\overrightarrow{\mathrm{MN}}-\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}=\left(\overrightarrow{\mathrm{HN}}-\overrightarrow{\mathrm{HM}}\right)-\left(\overrightarrow{{\mathrm{HN}}^{\text{'}}}-\overrightarrow{{\mathrm{HM}}^{\text{'}}}\right)$

$=\overrightarrow{\mathrm{HN}}-\overrightarrow{\mathrm{HM}}-\overrightarrow{{\mathrm{HN}}^{\text{'}}}+\overrightarrow{{\mathrm{HM}}^{\text{'}}}$

$=\left(\overrightarrow{\mathrm{HN}}-\overrightarrow{{\mathrm{HN}}^{\text{'}}}\right)+\left(\overrightarrow{{\mathrm{HM}}^{\text{'}}}-\overrightarrow{\mathrm{HM}}\right)=\overrightarrow{{\mathrm{N}}^{\text{'}}\mathrm{N}}+\overrightarrow{{\mathrm{MM}}^{\text{'}}}$

Khi đó ${\overrightarrow{\mathrm{MN}}}^2-{\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}}^2=\left(\overrightarrow{\mathrm{MN}}+\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}\right)\left(\overrightarrow{\mathrm{MN}}-\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}\right)$

$=2\overrightarrow{\mathrm{HK}}\left(\overrightarrow{{\mathrm{N}}^{\text{'}}\mathrm{N}}+\overrightarrow{{\mathrm{MM}}^{\text{'}}}\right)$

$=2\overrightarrow{\mathrm{HK}}.\overrightarrow{{\mathrm{N}}^{\text{'}}\mathrm{N}}+2\overrightarrow{\mathrm{HK}}.\overrightarrow{{\mathrm{MM}}^{\text{'}}}=2.0+2.0=0$

(do d là đường trung trực của MM’, NN’ nên $\overrightarrow{{\mathrm{MM}}^{\text{'}}}\perp \overrightarrow{\mathrm{HK}};\overrightarrow{{\mathrm{NN}}^{\text{'}}}\perp \overrightarrow{\mathrm{HK}}$).

Suy ra ${\overrightarrow{\mathrm{MN}}}^2={\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}}^2$

Do đó MN = M’N’ (2)

Từ (1) và (2) suy ra phép biến hình f bảo toàn khoảng cách giữa hai điểm bất kì.

Vậy f là một phép dời hình.

Bài 3 trang 10 Chuyên đề Toán 11: Cho phép dời hình f biến hình vuông ℋ có cạnh bằng 2 cm thành hình vuông ℋ ’. Tìm diện tích của ℋ ’.

Lời giải:

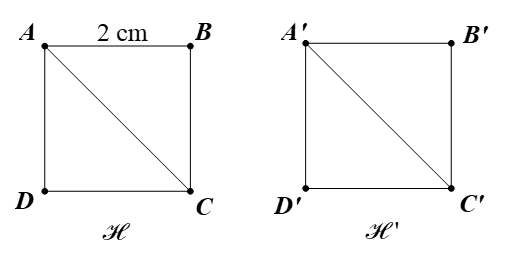
Giả sử ABCD là hình vuông ℋ.

Khi đó ta gọi A’B’C’D’ là hình vuông ℋ ’.

Theo hệ quả của phép dời hình, ta có phép dời hình f biến ∆ABC thành ∆A’B’C’ thỏa mãn ∆ABC = ∆A’B’C’.

Tương tự như vậy, ta có ∆ADC = ∆A’D’C’.

Ta có S_H’ = S_{∆A’B’C’} + S_{∆A’D’C’} = S_∆ABC + S_∆ADC = S_H = 2² = 4 (cm²).

Vậy diện tích của ℋ ’ bằng 4 cm².

Bài 4 trang 10 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, xét các phép biến hình sau đây:

– Phép biến hình f biến mỗi điểm M(x; y) thành điểm M’(–x; –y);

– Phép biến hình g biến mỗi điểm M(x; y) thành điểm M’(2x; 2y).

Trong hai phép biến hình trên, phép nào là phép dời hình? Giải thích.

Lời giải:

Lấy hai điểm bất kì M(x₁; y₁) và N(x₂; y₂).

Suy ra $\mathrm{MN}=\sqrt{{\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)}^2+{\left({\mathrm{y}}_2-{\mathrm{y}}_1\right)}^2}$.

– Ta có ảnh của M, N qua phép biến hình f lần lượt là M’(–x₁; –y₁), N’(–x₂; –y₂).

Khi đó ${\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}=\sqrt{{\left(-{\mathrm{x}}_2+{\mathrm{x}}_1\right)}^2+{\left(-{\mathrm{y}}_2+{\mathrm{y}}_1\right)}^2}=\sqrt{{\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)}^2+{\left({\mathrm{y}}_2-{\mathrm{y}}_1\right)}^2}=\mathrm{MN}$.

Vì vậy f là một phép dời hình.

– Ta có ảnh của M, N qua phép biến hình g lần lượt là M’(2x₁; 2y₁), N’(2x₂; 2y₂).

Khi đó ${\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}=\sqrt{{\left(2{\mathrm{x}}_2-2{\mathrm{x}}_1\right)}^2+{\left(2{\mathrm{y}}_2-2{\mathrm{y}}_1\right)}^2}=\sqrt{4{\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)}^2+4{\left({\mathrm{y}}_2-{\mathrm{y}}_1\right)}^2}$.

$=2\sqrt{{\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)}^2+{\left({\mathrm{y}}_2-{\mathrm{y}}_1\right)}^2}=2\mathrm{MN}\ne \mathrm{MN}$.

Vì vậy g không phải là một phép dời hình.

Vậy trong hai phép biến hình đã cho, phép dời hình là f.

Bài 5 trang 10 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, xét phép biến hình h biến mỗi điểm M(x; y) thành điểm M’(x; y), trong đó

Hãy chứng minh h là một phép dời hình.

Lời giải:

Lấy hai điểm bất kì M(x₁; y₁) và N(x₂; y₂).

Suy ra $\mathrm{MN}=\sqrt{{\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)}^2+{\left({\mathrm{y}}_2-{\mathrm{y}}_1\right)}^2}$.

Ta có ảnh của M, N qua phép biến hình h là ${\mathrm{M}}^{\text{'}}\left(\frac{\sqrt{2}}{2}{\mathrm{x}}_1-\frac{\sqrt{2}}{2}{\mathrm{y}}_1;\frac{\sqrt{2}}{2}{\mathrm{x}}_1+\frac{\sqrt{2}}{2}{\mathrm{y}}_1\right)$ và ${\mathrm{N}}^{\text{'}}\left(\frac{\sqrt{2}}{2}{\mathrm{x}}_2-\frac{\sqrt{2}}{2}{\mathrm{y}}_2;\frac{\sqrt{2}}{2}{\mathrm{x}}_2+\frac{\sqrt{2}}{2}{\mathrm{y}}_2\right)$

Khi đó

${\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}=\sqrt{{\left(\frac{\sqrt{2}}{2}{\mathrm{x}}_2-\frac{\sqrt{2}}{2}{\mathrm{y}}_2-\frac{\sqrt{2}}{2}{\mathrm{x}}_1+\frac{\sqrt{2}}{2}{\mathrm{y}}_1\right)}^2+{\left(\frac{\sqrt{2}}{2}{\mathrm{x}}_2+\frac{\sqrt{2}}{2}{\mathrm{y}}_2-\frac{\sqrt{2}}{2}{\mathrm{x}}_1-\frac{\sqrt{2}}{2}{\mathrm{y}}_1\right)}^2}$

$=\sqrt{\frac{1}{2}{\left({\mathrm{x}}_2-{\mathrm{y}}_2-{\mathrm{x}}_1+{\mathrm{y}}_1\right)}^2+\frac{1}{2}{\left({\mathrm{x}}_2+{\mathrm{y}}_2-{\mathrm{x}}_1-{\mathrm{y}}_1\right)}^2}$

$=\frac{\sqrt{2}}{2}.\sqrt{{\left[\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)-\left({\mathrm{y}}_2-{\mathrm{y}}_1\right)\right]}^2+{\left[\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)+\left({\mathrm{y}}_2-{\mathrm{y}}_1\right)\right]}^2}$

$=\frac{\sqrt{2}}{2}\sqrt{2{\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)}^2+2{\left({\mathrm{y}}_2-{\mathrm{y}}_1\right)}^2}$ (khai triển bình phương)

$=\sqrt{{\left({\mathrm{x}}_2-{\mathrm{x}}_1\right)}^2+{\left({\mathrm{y}}_2-{\mathrm{y}}_1\right)}^2}$

= MN

Vậy h là một phép dời hình.

Xem thêm các bài giải Chuyên đề học tập Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Phép tịnh tiến

Bài 3: Phép đối xứng trục

Bài 4: Phép đối xứng tâm

Bài 5: Phép quay

Bài 6: Phép vị tự