Cho điểm O trong mặt phẳng. Ta định nghĩa một phép biến hình h như sau: Với mỗi điểm M khác O chọn M’ = h(M
68
17/03/2024
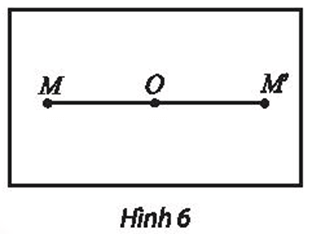
Thực hành 2 trang 8 Chuyên đề Toán 11: Cho điểm O trong mặt phẳng. Ta định nghĩa một phép biến hình h như sau: Với mỗi điểm M khác O chọn M’ = h(M) sao cho O là trung điểm của đoạn thẳng MM’ (Hình 6), còn với M trùng với O thì ta chọn O = h(M). Chứng minh h là một phép dời hình.
Trả lời
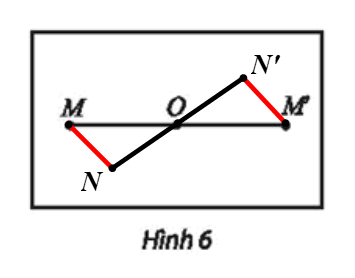
⦁ Với hai điểm M, N khác O, ta đặt M’ = h(M) và N’ = h(N) với O là trung điểm của MM’ và O cũng là trung điểm của NN’.
Suy ra tứ giác MNM’N’ là hình bình hành.
Do đó MN = M’N’ (1)
⦁ Với M trùng O, ta có O = h(M).
Suy ra MO = 0 (2)
Từ (1), (2), ta thu được h là một phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.
Vậy h là một phép dời hình.
Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Phép biến hình và phép dời hình
Bài 2: Phép tịnh tiến
Bài 3: Phép đối xứng trục
Bài 4: Phép đối xứng tâm
Bài 5: Phép quay
Bài 6: Phép vị tự


