Một người đã vẽ xong bức tranh một con thiên nga đang bơi trên mặt hồ (đường thẳng d) (Hình 7a

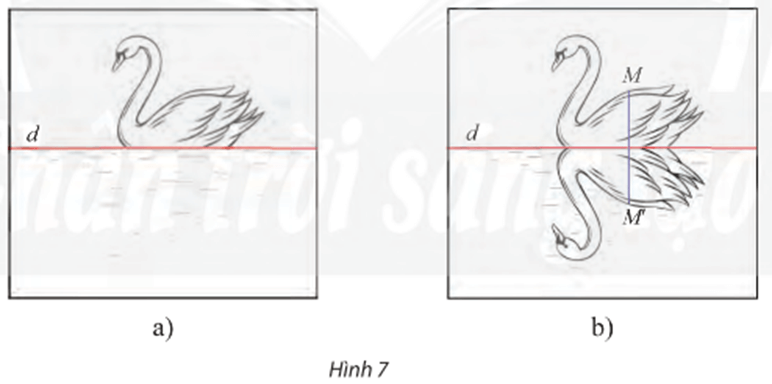
Vận dụng trang 8 Chuyên đề Toán 11: Một người đã vẽ xong bức tranh một con thiên nga đang bơi trên mặt hồ (đường thẳng d) (Hình 7a). Người đó muốn vẽ bóng của con thiên nga đó xuống mặt nước (như Hình 7b) bằng cách gấp tờ giấy theo đường thẳng d và đồ theo hình con thiên nga trên nửa tờ giấy còn lại. Chứng tỏ rằng đây là một phép dời hình.

Trả lời

Ta đặt f là phép biến hình biến con thiên nga trong bức tranh thành bóng của con thiên nga đó qua đường thẳng d (mặt hồ).

Chọn M’ = f(M) hay M’ là điểm đối xứng của M qua d.

Suy ra d là đường trung trực của đoạn thẳng MM’.

Gọi H là giao điểm của MM’ và d.

Khi đó H là trung điểm của MM’ và MM’ ⊥ d tại H.

Trên hình 7b, chọn điểm N tùy ý trên con thiên nga đã vẽ trên mặt hồ (như hình vẽ).

Chọn N’ = f(N) hay N’ là điểm đối xứng của N qua d.

Suy ra d là đường trung trực của đoạn thẳng NN’.

Gọi K là giao điểm của NN’ và d.

Khi đó K là trung điểm của NN’ và NN’ ⊥ d tại K.

Ta có $\overrightarrow{\mathrm{MN}}+\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}=\left(\overrightarrow{\mathrm{MH}}+\overrightarrow{\mathrm{HK}}+\overrightarrow{\mathrm{KN}}\right)+\left(\overrightarrow{{\mathrm{M}}^{\text{'}}\mathrm{H}}+\overrightarrow{\mathrm{HK}}+\overrightarrow{{\mathrm{KN}}^{\text{'}}}\right)$

$=\left(\overrightarrow{\mathrm{MH}}+\overrightarrow{{\mathrm{M}}^{\text{'}}\mathrm{H}}\right)+\left(\overrightarrow{\mathrm{KN}}+\overrightarrow{{\mathrm{KN}}^{\text{'}}}\right)+2\overrightarrow{\mathrm{HK}}$

$=\overrightarrow{0}+\overrightarrow{0}+2\overrightarrow{\mathrm{HK}}$ (do H, K lần lượt là trung điểm của MM’, NN’)

$=2\overrightarrow{\mathrm{HK}}$

Lại có $\overrightarrow{\mathrm{MN}}-\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}=\left(\overrightarrow{\mathrm{HN}}-\overrightarrow{\mathrm{HM}}\right)-\left(\overrightarrow{{\mathrm{HN}}^{\text{'}}}-\overrightarrow{{\mathrm{HM}}^{\text{'}}}\right)$

$=\overrightarrow{\mathrm{HN}}-\overrightarrow{\mathrm{HM}}-\overrightarrow{{\mathrm{HN}}^{\text{'}}}+\overrightarrow{{\mathrm{HM}}^{\text{'}}}$

$=\left(\overrightarrow{\mathrm{HN}}-\overrightarrow{{\mathrm{HN}}^{\text{'}}}\right)+\left(\overrightarrow{{\mathrm{HM}}^{\text{'}}}-\overrightarrow{\mathrm{HM}}\right)=\overrightarrow{{\mathrm{N}}^{\text{'}}\mathrm{N}}+\overrightarrow{{\mathrm{MM}}^{\text{'}}}$

Ta có ${\overrightarrow{\mathrm{MN}}}^2-{\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}}^2=\left(\overrightarrow{\mathrm{MN}}+\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}\right)\left(\overrightarrow{\mathrm{MN}}-\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}\right)=2\overrightarrow{\mathrm{HK}}\left(\overrightarrow{{\mathrm{N}}^{\text{'}}\mathrm{N}}+\overrightarrow{{\mathrm{MM}}^{\text{'}}}\right)$

$=2\overrightarrow{\mathrm{HK}}.\overrightarrow{{\mathrm{N}}^{\text{'}}\mathrm{N}}+2\overrightarrow{\mathrm{HK}}.\overrightarrow{{\mathrm{MM}}^{\text{'}}}=2.0+2.0=0$ (do MM’ ⊥ d và NN’ ⊥ d).

Suy ra ${\overrightarrow{\mathrm{MN}}}^2={\overrightarrow{{\mathrm{M}}^{\text{'}}{\mathrm{N}}^{\text{'}}}}^2$

Do đó MN = M’N’.

Vì vậy phép biến hình f bảo toàn khoảng cách giữa hai điểm bất kì.

Vậy ta có điều phải chứng minh.

Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Phép biến hình và phép dời hình

Bài 2: Phép tịnh tiến

Bài 3: Phép đối xứng trục

Bài 4: Phép đối xứng tâm

Bài 5: Phép quay

Bài 6: Phép vị tự