Giải bài tập Toán 7 Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc
Bài giảng Toán 7 Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc
Hoạt động khởi động
Giải Toán 7 trang 23 Tập 1
Lời giải:
Ta đã được học cách thực hiệp phép tính với phân số vì vậy ta sẽ đổi các số thập phân trong biểu thức trên ra phân số như sau:
0,5=510=120,5=510=12; 4,5=4510=924,5=4510=92.
Khi đó, ta có thể tính giá trị của biểu thức trên như sau:
0,5+4,5:3−316 . 430,5+4,5:3−316.43
=12+92:3−316 . 43=12+92:3−316.43
=12+92. 13−316 . 43=12+92.13−316.43
=12+32−14=12+32−14
=2−14=2−14
=84−14=84−14
=74.=74.
1. Thứ tự thực hiện các phép tính
Luyện tập 1 trang 23 Toán lớp 7 Tập 1: Tính giá trị của mỗi biểu thức sau:
b) 9 . (− 13)2−(− 0,1)3:2159.(−13)2−(−0,1)3:215.
Lời giải:
a) 0,2+2,5:72=15+52:720,2+2,5:72=15+52:72
=15+52 . 27=15+57=15+52.27=15+57
=1.75.7+5.57.5=735+2535=3235=1.75.7+5.57.5=735+2535=3235.
b) 9 . (− 13)2−(− 0,1)3:2159.(−13)2−(−0,1)3:215
=9 . 19−(−110)3:215=9.19−(−110)3:215
=1−−11000:215=1−−11000:215
=1+ 11000:215=1+11000:215
=1+ 11000 . 152=1+11000.152
=400400+ 3400=403400=400400+3400=403400.
Giải Toán 7 trang 24 Tập 1
Luyện tập 2 trang 24 Toán lớp 7 Tập 1: Tính giá trị của mỗi biểu thức sau:
a) (0,25−56) . 1,6+− 13(0,25−56).1,6+−13;
b) 3−2 . [0,5+(0,25−16)]3−2.[0,5+(0,25−16)].
Lời giải:
a) (0,25−56) . 1,6+− 13(0,25−56).1,6+−13
=(25100−56) . 85+− 13=(25100−56).85+−13
=(14−56) . 85+− 13=(14−56).85+−13
= 14. 85−56.85+− 13=14.85−56.85+−13
=25 − 43+− 13=25−43+−13
=25−(43+13)=25−(43+13)
=25−53=25−53
=615−2515=615−2515
=− 1915=−1915.
b) 3−2 . [0,5+(0,25−16)]3−2.[0,5+(0,25−16)]
=3−2 . [510+(25100−16)]=3−2.[510+(25100−16)]
=3−2 . [12+(14−16)]=3−2.[12+(14−16)]
=3−2 . [12+(312−212)]=3−2.[12+(312−212)]
=3−2 . (12+112)=3−2.(12+112)
=3−2 . 12−2.112=3−2.12−2.112
=3−1− 16=3−1−16
=2− 16=126−16=116=2−16=126−16=116.
2. Quy tắc dấu ngoặc
Giải Toán 7 trang 25 Tập 1
Luyện tập 3 trang 25 Toán lớp 7 Tập 1: Tính một cách hợp lí:
b) 12,5−1613+31312,5−1613+313.
Lời giải:
a) 1,8 −(37− 0,2)1,8−(37−0,2)
=1,8−37+0,2=1,8−37+0,2 (Quy tắc dấu ngoặc)
=1,8+0,2−37=1,8+0,2−37 (Tính chất giao hoán)
=2−37=2−37
=147−37=117=147−37=117.
b) 12,5−1613+31312,5−1613+313
=12,5+(−1613+313)=12,5+(−1613+313) (Quy tắc dấu ngoặc)
=12,5+−16+313=12,5+−16+313
= 12,5 – 1 = 11,5.
Luyện tập 4 trang 25 Toán lớp 7 Tập 1: Tính một cách hợp lí:
a) (− 56)−(− 1,8)+(− 16)−0,8(−56)−(−1,8)+(−16)−0,8;
b) (− 97)+(− 1,23)−(− 27)−0,77(−97)+(−1,23)−(−27)−0,77.
Lời giải:
a) (− 56)−(− 1,8)+(− 16)−0,8(−56)−(−1,8)+(−16)−0,8
= −56+1,8−16−0,8−56+1,8−16−0,8
=(− 56)+(− 16)+1,8−0,8=(−56)+(−16)+1,8−0,8 (Tính chất giao hoán)
=− ( 56+16)+(1,8−0,8)=−(56+16)+(1,8−0,8) (Quy tắc dấu ngoặc)
= (− 1) + 1
= 0 (Tính chất cộng với số đối)
b) (− 97)+(− 1,23)−(− 27)−0,77(−97)+(−1,23)−(−27)−0,77
=(− 97)− 1,23+27−0,77=(−97)−1,23+27−0,77 (Quy tắc dấu ngoặc)
=(− 97)+27− 1,23−0,77=(−97)+27−1,23−0,77 (Tính chất giao hoán)
=− (97− 27)−( 1,23+0,77)=−(97−27)−(1,23+0,77)
= (− 1) – 2
= – (1 + 2)
= – 3.
Bài tập
Bài 1 trang 25 Toán lớp 7 Tập 1: Tính:
a) 19−0,3 . 59+1319−0,3.59+13;
b) (− 23)2+16−(− 0,5)3(−23)2+16−(−0,5)3.
Lời giải:
a) 19−0,3 . 59+1319−0,3.59+13;
=19−310 . 59+13=19−310.59+13
=19−32.5. 53.3+13=19−32.5.53.3+13
=19−16+13=19−16+13
=218−318+618=518=218−318+618=518.
b) (− 23)2+16−(− 0,5)3(−23)2+16−(−0,5)3
=(− 2)232+16−(− 12)3=(−2)232+16−(−12)3
=49+16−(− 1)323=49+16−(−1)323
=49+16−− 18=49+16−−18
=49+16+ 18=49+16+18
=3272+1272+ 972=3272+1272+972
=5372=5372.
Bài 2 trang 25 Toán lớp 7 Tập 1: Tính:
d) 0,8: {0,2−7 . [16+(521−514)]}.
Lời giải:
a) (45−1):35−23 . 0,5
=(− 15):35−23 . 12
=−15. 53−23 . 12
=− 13−13
=− (13+13)=− 23.
b) 1−(59−23)2:427
=1−(59−69)2:427
=1−(− 19)2 . 274
=1−(− 1)292 . 274
=1−181 . 274
=1−127.3 . 274
=1−112=1112.
c) [(38−512) . 6+13] . 4
=[(924−1024) . 6+13] . 4
=(− 124 . 6+13) . 4
=(− 14+13) . 4
=(− 312+412) . 4
=112 . 4=13.
d) 0,8: {0,2−7 . [16+(521−514)]}
=45:{15−7 . [16+(1042−1542)]}
=45:{15−7 . [16+− 542]}
=45:{15−7 . [742+− 542]}
=45:{15−7 . 242}
=45:{15−7 . 22.3.7}
=45:{15− 13}
=45:{315− 515}
=45:− 215
=45 . − 152=− 6.
Giải Toán 7 trang 26 Tập 1
Bài 3 trang 26 Toán lớp 7 Tập 1: Chọn dấu “=”, “≠” thích hợp cho ? :
a) 289 . 0,7+289 . 0,5 ? 289 . (0,7+0,5);
b) 3613:4+3613:9 ? 3613:(4+9).
Lời giải:
a) Ta có: 289.0,7+289.0,5=9845+149=5615
Lại có: 289.(0,7+0,5)=289.1,2=5615
Do đó, 289 . 0,7+289 . 0,5 = 289 . (0,7+0,5)
Vậy 289 . 0,7+289 . 0,5 = 289 . (0,7+0,5)
b) Ta có 3613:4+3613:9=3613 . 14+3613 . 19
=3613 . (14+ 19)=3613 . (936+ 436)=3613 . 1336=1;
3613:(4+9)=3613:13=3613 . 113=36169.
Vì 1≠36169 nên 3613:4+3613:9 ≠ 3613:(4+9).
Vậy 3613:4+3613:9 ≠ 3613:(4+9).
Bài 4 trang 26 Toán lớp 7 Tập 1: Tính một cách hợp lí:
b) (− 36,75)+(3710−63,25)−(− 6,3);
d) (− 39,1) . 1325−60,9 . 1325.
Lời giải:
a) 415−(2,9−1115)
=415−2,9+1115 (Quy tắc dấu ngoặc)
=415+1115−2,9 (Tính chất giao hoán)
= 1 – 2,9
= – 1,9.
b) (− 36,75)+(3710−63,25)−(− 6,3)
=(− 36,75)+3710−63,25+ 6,3 (Quy tắc dấu ngoặc)
= (– 36,75) – 63,25 + 3,7 + 6,3 (Tính chất giao hoán)
= – (36,75 + 63,25) + (3,7 + 6,3) (Quy tắc dấu ngoặc)
= (– 100) + 10
= – 90.
c) 6,5+(− 1017)−(− 72)−717
=6,5− 1017+3,5−717 (Quy tắc dấu ngoặc)
=6,5+3,5− 1017−717 (Quy tắc dấu ngoặc)
=(6,5+3,5)− (1017+717) (Quy tắc dấu ngoặc)
= 10 – 1
= 9.
d) (− 39,1) . 1325−60,9 . 1325
=1325 . (−39,1−60,9)
= 1325 . (−100)
= –52.
Lời giải:
Số khóm hoa trồng được theo hai cạnh chiều dài là:
2.(5,5 : 0,25 + 1) = 46 (khóm hoa)
Số khóm hoa trồng được theo hai cạnh chiều rộng là:
2.(3,75 : 0,25 + 1) = 32 (khóm hoa)
Ta chú ý, mảnh vườn là hình chữ nhật nên theo cách tính này thì số khóm hoa ở 4 góc vườn của hình chữ nhật sẽ được tính 2 lần.
Do đó để tính được số khóm hoa được trồng dọc theo các cạnh của mảnh vườn, ta tính tổng số khóm hoa trồng được theo mỗi cạnh rồi trừ đi 4 (do ở mỗi góc, số khóm hoa được tính 2 lần).
Vậy số khóm hoa cần trồng là:
46 + 32 – 4 = 74 (khóm hoa)
a) Tính diện tích của miếng bìa.
b) Từ miếng bìa đó, người ta gấp thành một hình hộp chữ nhật. Tính thể tích của hình hộp chữ nhật.
Lời giải:
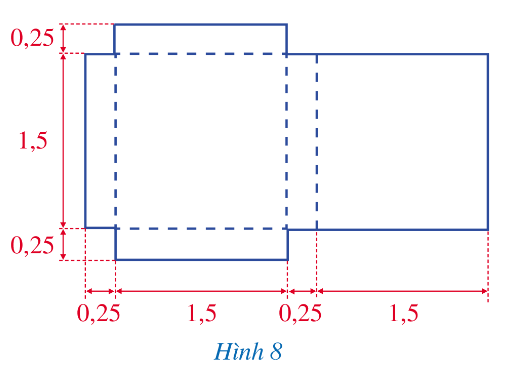
a) Đặt tên các điểm trên miếng lần lượt là A, B, C, D, E, F, G, H, I, K, L, M, N như hình vẽ:
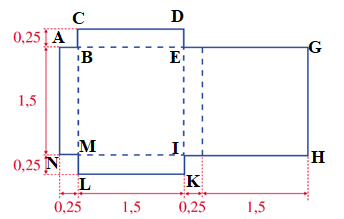
Ta có thể chia miếng bìa thành các hình nhỏ, sau đó tính tổng diện tích của các hình nhỏ đó.
Có nhiều các chia thành các hình nhỏ.
Chẳng hạn:
Ta chia miếng bìa đã cho thành 3 hình chữ nhật: ABMN, CDKL, EGHI.
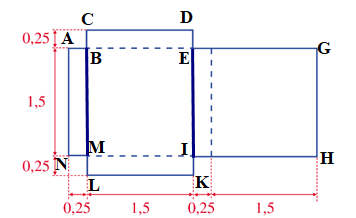
Diện tích hình chữ nhật ABMN là:
1,5 . 0,25 = 0,375 (dm2)
Chiều dài hình chữ nhật CDKL là:
0,25 + 1,5 + 0,25 = 2 (dm)
Diện tích hình chữ nhật CDKL là:
2 . 1,5 = 3 (dm2)
Chiều dài hình chữ nhật EGHI là:
1,5 + 0,25 = 1,75 (dm)
Diện tích hình chữ nhật EGHI là:
1,75 . 1,5 = 2,625 (dm2)
Diện tích miếng bìa đã cho là:
0,375 + 3 + 2,625 = 6 (dm2)
Vậy diện tích miếng bìa đã cho là 6 dm2.
b) Thể tích của hình hộp chữ nhật được gấp từ miếng bìa là:
1,5 . 1,5 . 0,25 = 0,5625 (dm3).
Vậy thể tích của hình hộp chữ nhật được gấp thành là 0,5625 dm3.
Lời giải:
• Lần giảm giá thứ nhất:
Cửa hàng giảm 5% giá niêm yết nên giá của chiếc ti vi lúc này bằng 100% – 5% = 95% giá niêm yết.
Giá của 1 chiếc ti vi sau lần giảm thứ nhất là:
20 000 000 . 95% = 19 000 000 (đồng)
• Lần giảm giá thứ hai:
Cửa hàng giảm thêm 2% giá của chiếc ti vi sau lần giảm thứ nhất nên giá của chiếc ti vi lúc này bằng 100% – 2% = 98% giá của chiếc ti vi sau lần giảm thứ nhất.
Giá của 1 chiếc ti vi sau lần giảm thứ hai là:
19 000 000. 98% = 18 620 000 (đồng)
Vậy khách hàng phải trả 18 620 000 đồng cho chiếc ti vi sau 2 lần giảm giá.
a) Tính số tiền chủ cửa hàng thu về khi bán hết số gạo đó.
b) Chủ cửa hàng đã lãi hay lỗ bao nhiêu phần trăm?
Lời giải:
a) Giá mua vào của 67 số sản phẩm là:
35 000 000 . 67 = 30 000 000 (đồng)
Giá mua vào của 17 số sản phẩm còn lại là:
35 000 000 – 30 000 000 = 5 000 000 (đồng)
Vì 67 số sản phẩm được bán với giá bán mỗi sản phẩm cao hơn 10% so với giá mua vào nên số tiền lãi thu về là:
30 000 000 .10% = 3 000 000 (đồng)
Số tiền thu về khi bán 67 số sản phẩm đó là:
30 000 000 + 3 000 000 = 33 000 000 (đồng)
Vì 17 số sản phẩm còn lại được bán với giá bán mỗi sản phẩm thấp hơn 25% so với giá mua vào nên số tiền bị lỗ là:
5 000 000 . 25% = 1 250 000 (đồng)
Số tiền thu về khi bán 17 số sản phẩm còn lại là:
5 000 000 – 1 250 000 = 3 750 000 (đồng)
Số tiền chủ cửa hàng thu về khi bán hết số sản phẩm đó là:
33 000 000 + 3 750 000 = 36 750 000 (đồng)
Vậy số tiền chủ cửa hàng thu về khi bán hết số sản phẩm đó là 36 750 000 đồng.
b) Vì chủ cửa hàng lãi được 3 000 000 đồng khi bán 67 số sản phẩm và lỗ 1 250 000 đồng khi bán 17 số sản phẩm còn lại.
Mà 3 000 000 đồng > 1 250 000 đồng
Nên chủ cửa hàng đã lãi số tiền là:
3 000 000 – 1 250 000 = 1 750 000 (đồng)
Số phần trăm chủ cửa hàng đã lãi là:
1 750 00035 000 000 . 100 %=5 %
Vậy chủ cửa hàng đã lãi 5%.
Xem thêm lời giải bài tập SGK Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 2: Cộng, trừ, nhân, chia số hữu tỉ
Bài 3: Phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ