Viết phương trình tiếp tuyến của parabol y = –x^2 + 4x, biết

Bài 9.3 trang 86 Toán 11 Tập 2: Viết phương trình tiếp tuyến của parabol y = –x² + 4x, biết:

a) Tiếp điểm có hoành độ x₀ = 1;

b) Tiếp điểm có tung độ y₀ = 0.

Trả lời

Đặt y = f(x) = – x² + 4x.

Với x₀ bất kì, ta có:

f'(x₀) = $\underset{x\to x_0}{\lim }\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{-x^2+4x+{x_0}^2-4x_0}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{-\left(x^2-{x_0}^2\right)+4\left(x-x_0\right)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{\left(x-x_0\right)\left(-x-x_0+4\right)}{x-x_0}$

$=\underset{x\to x_0}{\lim }(-x-x_0+4)=-2x_0+4$.

Vậy hàm số y = –x² + 4x có đạo hàm là hàm số y' = –2x + 4.

a)

Ta có: y'(1) = –2.1 + 4 = 2.

Ngoài ra, f(1) = 3 nên phương trình tiếp tuyến cần tìm là:

y – 3 = 2(x – 1) hay y = 2x + 1.

b)

Ta có: y₀ = 0 nên –x₀² + 4x₀ = 0 ⇔ .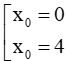

+) Với x₀ = 0, y₀ = 0, ta có y'(0) = 4, do đó phương trình tiếp tuyến cần tìm là y = 4x.

+) Với x₀ = 4, y₀ = 0, ta có y'(4) = –4 do đó phương trình tiếp tuyến cần tìm là:

y = –4(x – 4) hay y = –4x + 16.

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác: