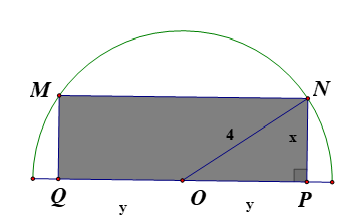
Từ một miếng tôn hình bán nguyệt có bán kínhR=4 , người ta muốn cắt một hình chữ nhật (xem hình vẽ) có diện tích lớn nhất. Diện tích lớn nhất có thể của miếng tôn hình chữ nhật bằng

Chọn D

Gọi chiều rộng của hình chữ nhật là $x,0<x\le 4$.

                    Chiều dài của hình chữ nhật là $2y,y>0$.

                    Xét $\Delta ONP$ vuông tạ P ta có $x^2+y^2=16\Rightarrow y=\sqrt{16-x^2}$.

Diện tích hình chữ nhật MNPQ  là

 $S_{MNPQ}=x\mathrm{.2.}\sqrt{16-x^2}=2.x.\sqrt{16-x^2}\le 2.\frac{x^2+16-x^2}{2}=16$.

                    Vậy diện tích lớn nhất của hình chữ nhật là 16 (đvdt).