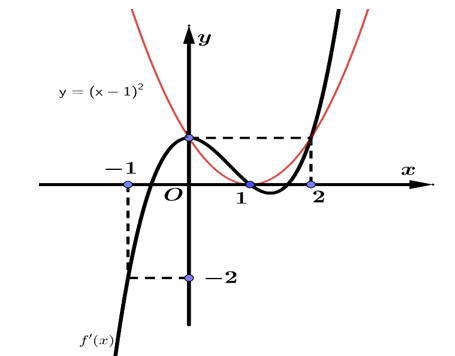
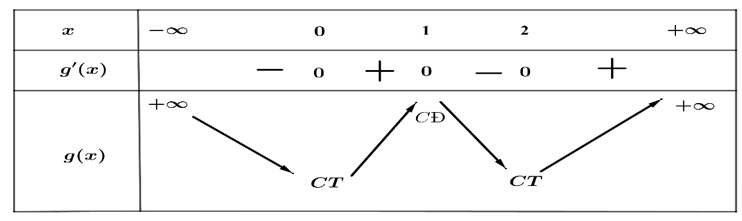
Cho hàm số y=f(x) có đạo hàm trên R. Đồ thị hàm số y=f'(x) như hình vẽ bên dưới. Hàm số g(x)=f(x)= -x^3/3+x^2-x+2 có bao nhiêu điểm cực đại?
Cho hàm số y=f(x) có đạo hàm trên R. Đồ thị hàm số y=f'(x) như hình vẽ bên dưới.
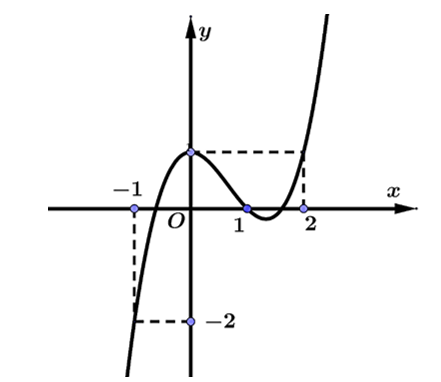
Hàm số g(x)=f(x)−x33+x2−x+2 có bao nhiêu điểm cực đại?
A. 0
B. 1
C. 2
D. 3