Cho hình chóp SABCcó các cạnh AB=a, AC = a căn 3, SB> 2a
Cho hình chóp SABCcó các cạnh AB=a, , và góc . Biết sin của góc giữa đường thẳng SBvà mặt phẳng bằng . Tính thể tích khối chóp SABC
A.
B.
C.
D.
Cho hình chóp SABCcó các cạnh AB=a, , và góc . Biết sin của góc giữa đường thẳng SBvà mặt phẳng bằng . Tính thể tích khối chóp SABC
A.
B.
C.
D.
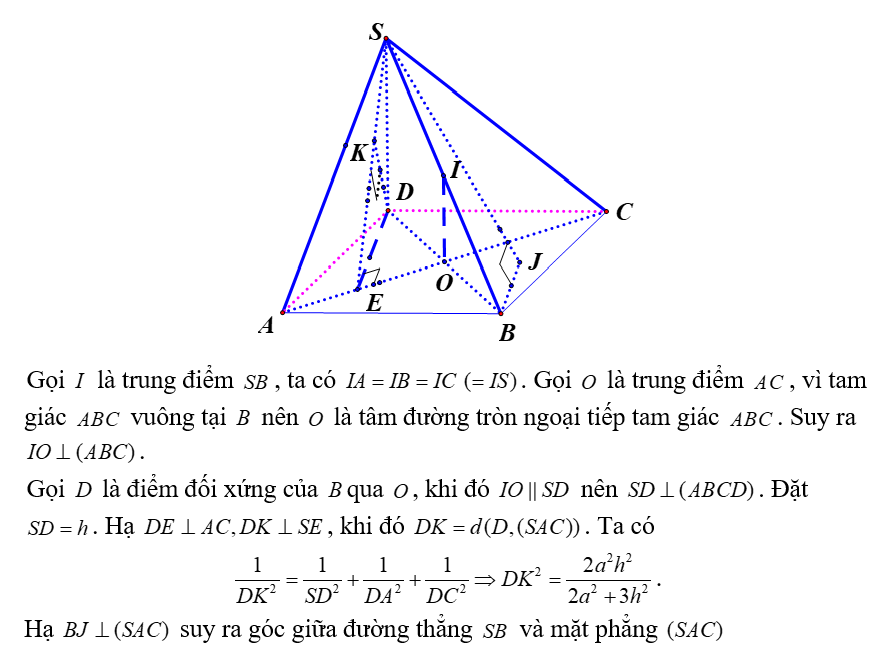
là góc . Ta có .
Ta thấy . Do đó
hoặc .
Trong tam giác vuông SDB có , nên , hay h>a. Suy ra .Vậy .