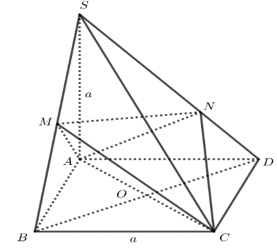
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a,SA= a và SA vuông góc với đáy. Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho $SN=2ND$. Tính thể tích V của khối tứ diện ACMN.

Ta có: $V_{S.ABCD}=\frac{1}{3}SA.S_{S.ABCD}=\frac{a^3}{3}$.

Vì $\frac{ND}{SD}=\frac{1}{3}\Rightarrow d\left(N,\left(ABCD\right)\right)=\frac{1}{3}SA=\frac{a}{3}$.

$\frac{MB}{SB}=\frac{1}{2}\Rightarrow d\left(M,\left(ABCD\right)\right)=\frac{1}{2}SA=\frac{a}{2}$.

Mà $V_{ACMN}=V_{S.ABCD}-V_{SAMN}-V_{SCMN}-V_{MABC}-V_{NADC}$

Mặt khác $V_{SABD}=V_{SBCD}=\frac{1}{2}{V}_{S.ABCD}=\frac{a^3}{6}$.

$\frac{V_{SAMN}}{V_{SABD}}=\frac{SM}{SB}.\frac{SN}{SD}=\frac{1}{2}.\frac{2}{3}=\frac{1}{3}\Rightarrow V_{S.AMN}=\frac{1}{3}{V}_{SABC}=\frac{1}{3}.\frac{a^3}{6}=\frac{a^3}{18}$.

$\frac{V_{SCMN}}{V_{SBCD}}=\frac{SM}{SB}.\frac{SN}{SD}=\frac{1}{2}.\frac{2}{3}=\frac{1}{3}\Rightarrow V_{SCMN}=\frac{1}{3}{V}_{SBCD}=\frac{1}{3}.\frac{a^3}{6}=\frac{a^3}{18}$.

$V_{MABC}=\frac{1}{3}d\left(M,\left(ABCD\right)\right).S_{ABC}=\frac{1}{3}.\frac{a}{2}.\frac{1}{2}{a}^2=\frac{a^3}{12}$.

$V_{NADC}=\frac{1}{3}d\left(N,\left(ABCD\right)\right).S_{ADC}=\frac{1}{3}.\frac{a}{3}.\frac{1}{2}{a}^2=\frac{a^3}{18}$.

Vậy $V_{ACMN}=\frac{a^3}{3}-\frac{a^3}{18}-\frac{a^3}{18}-\frac{a^3}{12}-\frac{a^3}{18}=\frac{a^3}{12}$.