Từ một điểm M ở ngoài đường tròn (O), vẽ hai tiếp tuyến MA, MB đến đường tròn (A, B là hai tiếp điểm). Qua A vẽ đường thẳng song song với MB, cắt đường tròn tại E, đoạn thẳng ME cắt đường tròn tại F. Hai đường thẳng AF và MB cắt nhau tại I.
a) Chứng minh tứ giác MAOB nội tiếp đường tròn.
b) Chứng minh \(I{B^2} = IF.IA.\)
c) Chứng minh IB = IM.
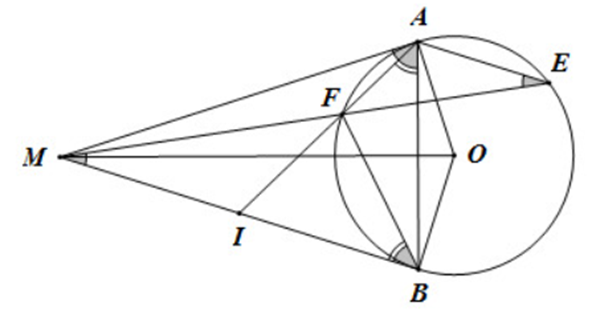
a) Vì MA, MB là tiếp tuyến của (O) nên MA ⊥ AO, MB ⊥ BO.
⇒ \(\widehat {MAO} = \widehat {MBO} = 90^\circ \)
⇒ \(\widehat {MAO} + \widehat {MBO} = 180^\circ \)
⇒ MAOB là tứ giác nội tiếp đường tròn (dpcm)
b) Ta có: \(\widehat {FAB} = \widehat {FBI}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BF)
Xét \(\Delta IAB\) và \(\Delta IBF\) có:
\(\widehat {IAB} = \widehat {IBF}\left( {cmt} \right)\)
\(\widehat {AIB}\) chung
Do đó \(\Delta IAB\) ᔕ \(\Delta IBF\left( {g.g} \right)\)
Suy ra \(\frac{{IA}}{{IB}} = \frac{{IB}}{{IF}}\) hay IB2 = IA.IF.
c) Ta có: \(\widehat {MAI} = \widehat {AEF}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AF)
Vì AE // MB nên \(\widehat {AEF} = \widehat {FMI}\)
Suy ra \(\widehat {MAI} = \widehat {FMI}\)
Xét \(\Delta MAI\) và \(\Delta FMI\) có:
\(\widehat {MAI} = \widehat {FMI}\,\,\left( {cmt} \right)\)
\(\widehat {MIA}\) chung
Do đó \(\Delta MAI\) ᔕ \(\Delta FMI\,\,\left( {g.g} \right)\)
Suy ra \(\frac{{MI}}{{FI}} = \frac{{AI}}{{MI}}\) hay IM2 = IA.IF.
Kết hợp với ý b ta có IB2 = IM2 = IA.IF ⇒ IB = IM (dpcm)