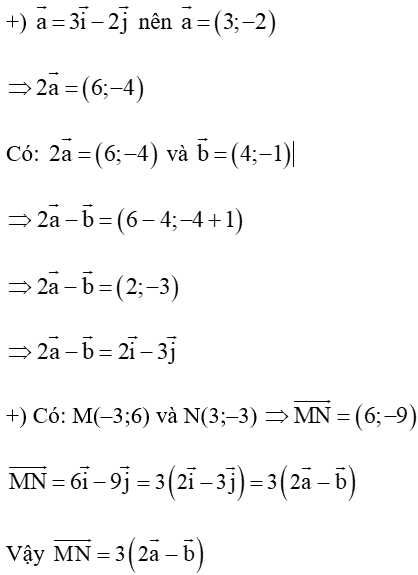Trong mặt phẳng tọa độ Oxy, cho các vectơ a = 3i - 2j; vecto b = (4;-1) và các điểm M(‒3;6), N(3;‒3).

Bài 4.17 trang 65 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các vectơ $\overrightarrow{a}=3\overrightarrow{i}-2\overrightarrow{j};$$\overrightarrow{b}=\left(4;-1\right)$ và các điểm M(‒3;6), N(3;‒3).

a) Tìm mối liên hệ giữa các vectơ $\overrightarrow{MN}$ và $2\overrightarrow{a}-\overrightarrow{b}.$

b) Các điểm O, M, N có thẳng hàng hay không?

c) Tìm điểm P(x;y) để OMNP là hình bình hành.

Trả lời

a) Ta có:

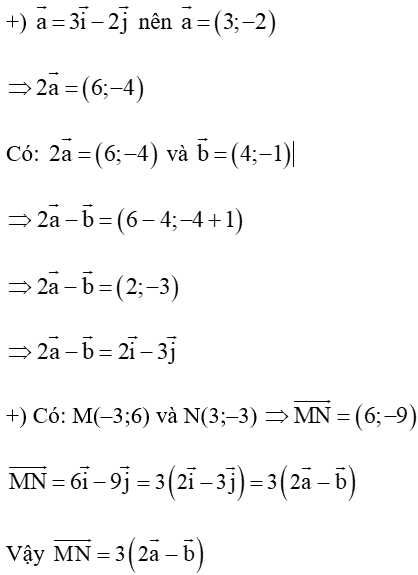
b) Ta có

+ M(-3; 6)$\Rightarrow \overrightarrow{OM}=\left(-3;6\right)$

+) N(3;‒3) $\Rightarrow \overrightarrow{ON}=\left(3;-3\right)$

Hai vectơ $\overrightarrow{OM}=\left(-3;6\right),\overrightarrow{ON}=\left(3;-3\right)$ không cùng phương (vì $\frac{-3}{3}\ne \frac{6}{-3}$).

Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.

Vậy ba điểm O, M, N không thẳng hàng.

c)

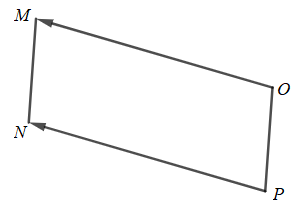
Các điểm O, M, N không thẳng hàng, tứ giác OMNP là hình bình hành khi và chỉ khi $\overrightarrow{OM}=\overrightarrow{PN}$

Ta có: M(‒3;6); N(3;‒3) và P(x; y)

$\Rightarrow \overrightarrow{OM}=\left(-3;6\right),\overrightarrow{PN}=\left(3-x;-3-y\right)$ 

Do đó $\overrightarrow{OM}=\overrightarrow{PN}$

$\iff \left\{\begin{array}{l}-3=3-x\\ 6=-3-y\end{array}\right.\iff \left\{\begin{array}{l}x=6\\ y=-9\end{array}\right.\Rightarrow P\left(6;-9\right).$

Vậy điểm cần tìm là P(6;‒9).

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vecto với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vecto

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số