Trong không gian với hệ tọa độ Oxyz cho điểm $A(-2;2;-2)$ và điểm $B(3;-3;3)$. Điểm M thay đổi trong không gian thỏa mãn $\frac{MA}{MB}=\frac{2}{3}.$ Điểm $N(a;b;c)$ thuộc mặt phẳng $\left(P\right):-x+2y-2z+6=0$ sao cho MN nhỏ nhất. Tính tổng $T=a+b+c$.

A. 6. 

B. -2. 

C. 12.

D. -6.

Gọi $M(x;y;z).$ Ta có $\frac{MA}{MB}=\frac{2}{3}$
$\iff 9M{A}^2=4M{B}^2\iff {(x+6)}^2+\stackrel{MB}{{(y-6)}^2}+{(z+6)}^2=108.$
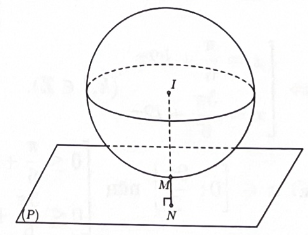
Vậy điểm M thuộc mặt cầu tầm $I(-6;6;-6),$ bán kính $R=6\sqrt{3}.$
Vậy MN nhỏ nhất khi M, N thuộc đường thẳng đi qua tâm I và vuông góc với mặt phẳng (P).  Gọi (d) là đường thẳng đi qua tâm I và vuông góc với mặt phẳng (P)
Khi đó $\left(d\right):\left\{\begin{array}{l}x=-6-t\\ y=6+2t\\ z=-6-2t\end{array}\right..$
Tọa độ điểm N là nghiệm của hệ phương trình
$\left\{\begin{array}{l}x=-6-t\\ y=6+2t\\ z=-6-2t\\ -x+2y-2z+6=0\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-6-t\\ y=6+2t\\ z=-6-2t\\ 6+t+12+4t+12+4t+6=0\end{array}\iff \left\{\begin{array}{l}x=-2\\ y=-2\\ z=2\\ t=-4\end{array}.\Rightarrow N(-2;-2;2).\right.\right.$
Do đó $T=-2-2+2=-2$

Chọn B