Cho hình chóp S.ABCD có đáy là hình chữ nhật, biết AB = 2a, AD = a, SA = 3a
6
26/11/2024
Cho hình chóp S.ABCD có đáy là hình chữ nhật, biết AB = 2a, AD = a, SA = 3a và SA vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh CD, điểm sao cho SE = a, cosin của góc giữa hai mặt phẳng (SAC) và (BME) bằng
A.
B.
C.
D.
Trả lời
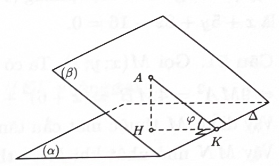
Góc giữa hai mặt phẳng và là góc Khi đó Gọi điểm G là trọng tâm kéo dài tia BM cắt AD tại F.
Ta có
Khi đó góc giữa hai mặt phẳng và là góc có
Ta có
Chọn B
