Trong không gian Oxyz, cho hai điểm A(0;0;10) và $B\left(3;4;\frac{19}{2}\right)$. Xét các điểm M thay đổi sao cho tam giác OAM không phải là tam giác nhọn và có diện tích bằng 20. Giá trị nhỏ nhất của độ dài đoạn thẳng MB thuộc khoảng nào dưới đây?

Đáp án đúng là: D

Ta có: $S_{OAM}=\frac{1}{2}OA.d\left(M;OA\right)=20\Rightarrow d\left(M;OA\right)=4.$

Suy ra: M di động trên mặt trụ, bán kính bằng 4 trục là OA

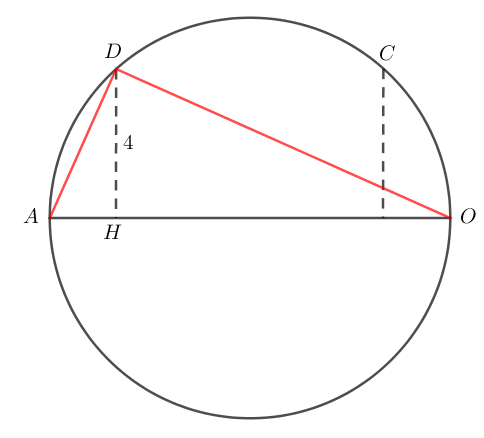
Xét điểm D như hình vẽ, $\left\{\begin{array}{l}HA.HO=H{D}^2=16\\ HA+HO=10\end{array}\right.\Rightarrow \left\{\begin{array}{l}HA=2\\ HO=8\end{array}\right..$

· Trường hợp 1: Nếu tam giác OAM là tam giác có góc $\widehat{AMO}\ge 90°$ thì điểm M chạy trên đoạn EF, khi đó BM có giá trị nhỏ nhất bằng $BF=\frac{\sqrt{13}}{2}$.

· Trường hợp 2: Nếu tam giác OAM là tam giác có góc $\widehat{MAO}\ge 90°$ thì điểm M chạy trên tia CD, khi đó BM có giá trị nhỏ nhất bằng $BC=\frac{\sqrt{5}}{2}$.

· Trường hợp 3: Nếu tam giác OAM là tam giác có góc $\widehat{MOA}\ge 90°$ thì điểm M chạy trên tia GH, khi đó BM có giá trị nhỏ nhất bằng $BG=\frac{\sqrt{365}}{2}$.

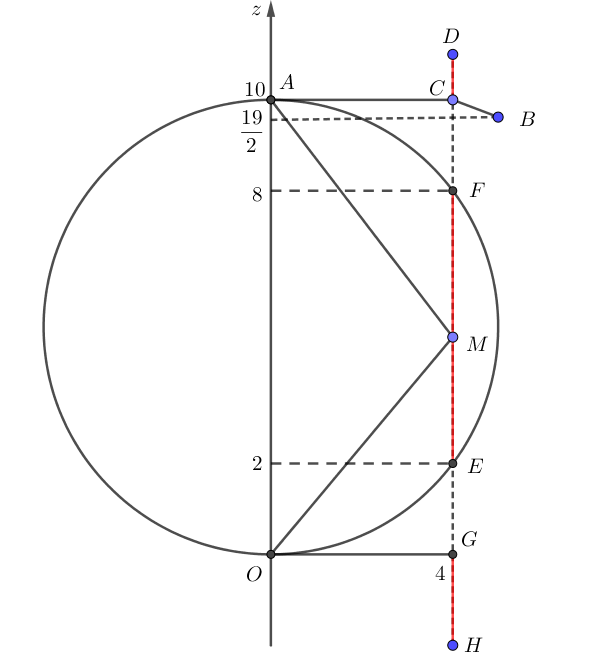
So sánh ba trường hợp trên ta thấy $B{M}_{\min }=\frac{\sqrt{5}}{2}\approx \mathrm{1,118033989}\in \left(0;\frac{3}{2}\right)$.