Cho tứ diện ABCD có AB = a, AC = a căn 5, góc DAB = góc CBD = 90 độ , góc ABC = 135 độ. Biết góc giữa hai mặt phẳng (ABD) và (BCD)

A. $\frac{a^3}{\sqrt{2}}$

B. $\frac{a^3}{3\sqrt{2}}$

C. $\frac{a^3}{2\sqrt{3}}$

D. $\frac{a^3}{6}$

Trả lời

Đáp án đúng là: D

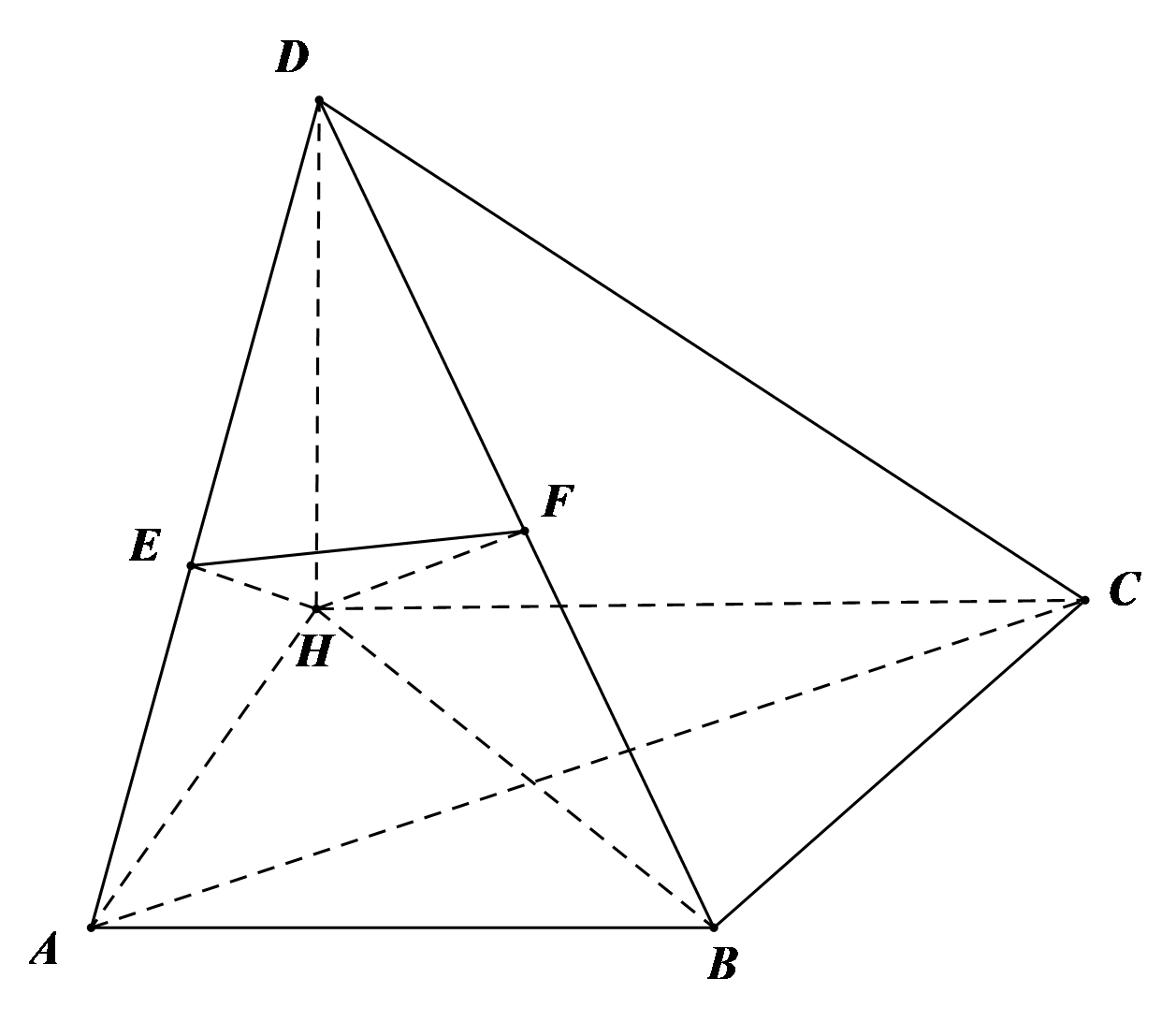
Dựng $DH\perp \left(ABC\right)$.

Ta có $\left\{\begin{array}{l}BA\perp DA\\ BA\perp DH\end{array}\Rightarrow BA\perp AH\right.$. Tương tự $\left\{\begin{array}{l}BC\perp DB\\ BC\perp DH\end{array}\Rightarrow BC\perp BH\right.$.

Tam giác AHB có $AB=a,\widehat{ABH}=45°\Rightarrow \Delta HAB$ vuông cân tại $A\Rightarrow AH=AB=a$.

Áp dụng định lý côsin, ta có $BC=a\sqrt{2}$.

Vậy $S_{△ABC}=\frac{1}{2}\cdot BA\cdot BC\cdot \sin \widehat{CBA}=\frac{1}{2}\cdot a\cdot a\sqrt{2}\cdot \frac{\sqrt{2}}{2}=\frac{a^2}{2}$.

Dựng $\left\{\begin{array}{l}HE\perp DA\\ HF\perp DB\end{array}\Rightarrow HE\perp \left(DAB\right)\right.$ và $HF\perp \left(DBC\right)$.

Suy ra $\widehat{\left(\left(DBA\right),\left(DBC\right)\right)}=\widehat{(HE,HF})=\widehat{EHF}$ và tam giác HEF vuông tại E.

Đặt DH = x, khi đó $HE=\frac{ax}{\sqrt{a^2+x^2}},HF=\frac{xa\sqrt{2}}{\sqrt{2a^2+x^2}}$.

Suy ra $\cos \widehat{EHF}=\frac{HE}{HF}=\sqrt{\frac{3}{4}}=\frac{\sqrt{x^2+2a^2}}{\sqrt{2x^2+2a^2}}\Rightarrow x=a$.

Vậy $V_{ABCD}=\frac{1}{3}\cdot DH\cdot S_{\Delta ABC}=\frac{a^3}{6}$.